题目内容
要测量顶部不能到达的电视塔AB的高度, 在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD="120°," CD="40m," 则电视塔的高度为


A.10 m m | B.20m | C.20 m m | D.40m |
D
试题分析:解:由题可设AB=x,则 BD=
 x , BC=x,在△DBC中,∠BCD=120°,CD=40,由余弦定理得BD2=BC2+CD2-2BC•CD•cos∠DCB,即:(
x , BC=x,在△DBC中,∠BCD=120°,CD=40,由余弦定理得BD2=BC2+CD2-2BC•CD•cos∠DCB,即:( x)2=(40)2+x2-2×40•x•cos120°,整理得:x2-20x-800=0,解得x=40或x=-20(舍),所以,所求塔高为40米
x)2=(40)2+x2-2×40•x•cos120°,整理得:x2-20x-800=0,解得x=40或x=-20(舍),所以,所求塔高为40米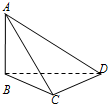 .
.故选D.
点评:本题主要考查了解三角形的实际应用.考查了运用数学知识,建立数学模型解决实际问题的能力.

练习册系列答案
相关题目
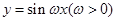 的部分如图所示,点A、B是最高点,点C是最低点,若
的部分如图所示,点A、B是最高点,点C是最低点,若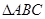 是直角三角形,则
是直角三角形,则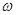 的值为
的值为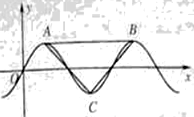
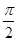 B.
B.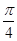 C.
C.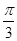 D.
D.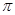
 中,若AC=1,
中,若AC=1, ,
,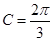 ,则BC= .
,则BC= . 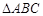 是锐角三角形,
是锐角三角形,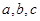 分别是内角A、B、C所对边长,并且
分别是内角A、B、C所对边长,并且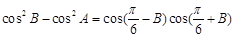 .
.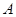 ;
;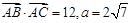 ,且
,且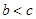 ,求边
,求边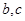 .
. 是第二象限的角,
是第二象限的角, ,则
,则 .
. 的角A、B、C所对的边分别为
的角A、B、C所对的边分别为 ,已知
,已知
 中,角A.、B、C的对边分别为
中,角A.、B、C的对边分别为 、
、 、
、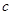 .角A.、B、C成等差数列。
.角A.、B、C成等差数列。 的值; (2)边
的值; (2)边 的值。
的值。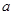 、
、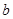 、
、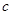 所对的角分别为A、B、C,则
所对的角分别为A、B、C,则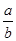 的范围是 。
的范围是 。 ,则cosC= .
,则cosC= .