题目内容
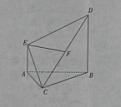
(12分)如图,四边形ABCD是矩形,PA⊥平面ABCD,其中AB=3,PA=4,
若在线段PD上存在点E 使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只
使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只
有一个点E使得BE⊥CE时,二面角E—BC—A正切值的大小。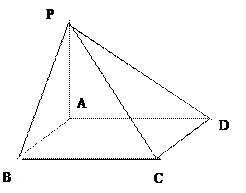

若以BC为直径的球面与线段PD有交点E,由于点E与BC确定的平面与球的截
面是一个大圆,则必有BE⊥CE,因此问题转化为以BC为直径的球与线段PD有交点。
设BC的中点为O(即球心),再取AD的中点M,易知OM⊥平面PAD,作ME⊥PD交PD于点E,连结OE,则OE⊥PD,所以OE即为点O到直线PD的距离,又因为OD>OC,OP>OA>OB,点P,D在球O外,所以要使以BC为直径的球与线段PD有交点,只要使OE≤OC(设OC=OB=R)即可。
由于△DEM∽△DAP,可求得ME=  ,
,
所以OE2="9+" 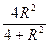 令OE2≤R2,即9+
令OE2≤R2,即9+ 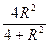 ≤R2,解之得R≥2
≤R2,解之得R≥2 ;
;
所以AD=2R≥4 ,所以AD的取值范围[ 4
,所以AD的取值范围[ 4 ,+∞
,+∞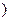 ,
,
当且仅当AD= 4 时,点E在线段PD上惟一存在,此时易求得二面角E—BC—A的平面角正切值为
时,点E在线段PD上惟一存在,此时易求得二面角E—BC—A的平面角正切值为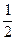 。
。
解析

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k等于( )
| A.2 | B.-4 | C.4 | D.-2 |
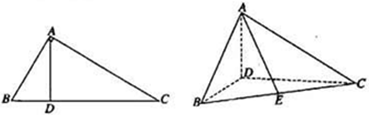
 中,
中, 是
是 上的高,沿
上的高,沿 把
把 折起,使
折起,使 。
。
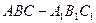 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱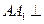 面
面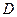 是
是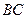 的中点.
的中点.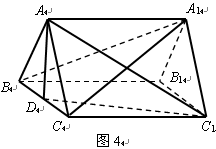
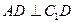 ;
;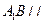 平面
平面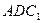 .
. ,求证:
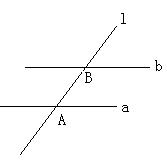
,求证: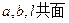 .
.
 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
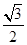 B.
B.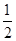 C.
C. D.
D.