题目内容
(本题满分12分)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆右顶点到直线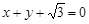 的距离为
的距离为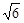 ,离心率
,离心率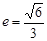
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A为椭圆与y轴负半轴的交点,设直线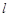 :
: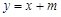 ,是否存在实数m,使直线
,是否存在实数m,使直线 与(Ⅰ)中的椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
与(Ⅰ)中的椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
(1) 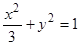 (2) m=2
(2) m=2
解析试题分析:解(Ⅰ)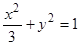
(Ⅱ) 过A且垂直
过A且垂直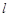 的直线为
的直线为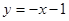 ,若存在m使∣AM∣=∣AN∣,则
,若存在m使∣AM∣=∣AN∣,则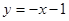 应为线段MN的垂直平分线,即MN的中点应在直线
应为线段MN的垂直平分线,即MN的中点应在直线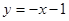 上,
上,
联立 得
得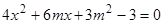 ,
,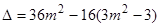 ①
①
MN中点坐标为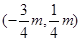 ,带入
,带入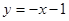 得
得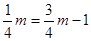 ∴m=2 将m=2代入①中得
∴m=2 将m=2代入①中得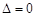 ,所以不存在m使∣AM∣=∣AN∣
,所以不存在m使∣AM∣=∣AN∣
考点:椭圆的方程以及直线与椭圆的位置关系
点评:解决该试题的关键是利用性质得到a,b,c的关系式,同时能结合联立方程组,韦达定理来得到参数m的值,属于基础题。

练习册系列答案
相关题目
 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,
轴交于点B,且与一条渐近线交于点C,点O为坐标原点, ,
,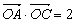 ,过点F的直线
,过点F的直线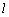 与双曲线右支交于点
与双曲线右支交于点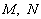 .
.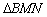 面积的最小值.
面积的最小值.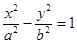 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆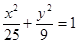 的焦点相同,求双曲线的方程及焦点坐标。
的焦点相同,求双曲线的方程及焦点坐标。 :
: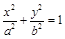 (
(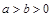 )过点
)过点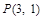 ,其左、右焦点分别为
,其左、右焦点分别为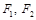 ,且
,且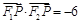 .
.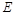 的方程;
的方程;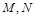 是直线
是直线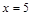 上的两个动点,且
上的两个动点,且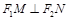 ,则以
,则以 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.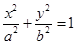 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.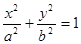 (
(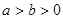 )过点
)过点 (0,2),离心率
(0,2),离心率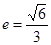 .
. (2,0)的直线
(2,0)的直线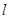 与椭圆相交于
与椭圆相交于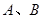 两点,且
两点,且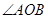 为锐角(其中
为锐角(其中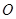 为坐标原点),求直线
为坐标原点),求直线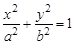
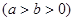 的一个顶点为B
的一个顶点为B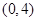 ,离心率
,离心率
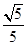 ,
,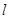 的方程.
的方程. 为极点,
为极点,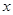 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线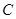 的极坐标方程是
的极坐标方程是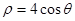 ,直线
,直线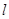 的参数方程是
的参数方程是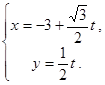 (
( 为参数)。
为参数)。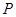 的极坐标;
的极坐标; 、
、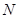 分别为曲线
分别为曲线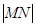 的最小值。
的最小值。 (其中
(其中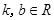 且
且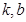 为常数)的图像经过点A
为常数)的图像经过点A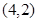 、B
、B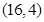 .
.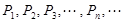 是函数
是函数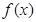 图像上的点,
图像上的点,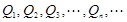 是
是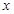 正半轴上的点.
正半轴上的点.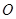 为坐标原点,
为坐标原点,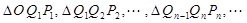 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列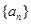 的通项公式;
的通项公式;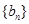 满足
满足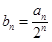 ,记
,记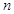 项和为
项和为 ,证明:
,证明: 。
。