题目内容
8.数列{an}中,a1=1,an=$\frac{{a}_{n-1}}{1+3{a}_{n-1}}$(n≥2),则数列{an}的通项公式为$\frac{1}{3n-2}$.分析 通过对等式an=$\frac{{a}_{n-1}}{1+3{a}_{n-1}}$(n≥2)两边同时取倒数、整理可知$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n-1}}$+3(n≥2),进而可知数列{$\frac{1}{{a}_{n}}$}是以1为首项、3为公差的等差数列,计算即得结论.
解答 解:∵an=$\frac{{a}_{n-1}}{1+3{a}_{n-1}}$(n≥2),
∴$\frac{1}{{a}_{n}}$=$\frac{1+3{a}_{n-1}}{{a}_{n-1}}$=$\frac{1}{{a}_{n-1}}$+3(n≥2),
又∵$\frac{1}{{a}_{1}}$=1,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项、3为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=1+3(n-1)=3n-2,
∴an=$\frac{1}{3n-2}$,
故答案为:$\frac{1}{3n-2}$.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
16.在△ABC中,已知a-b=ccosB-ccosA,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等腰或直角三角形 |
17.执行如图所示的程序框图输出的结果为( )
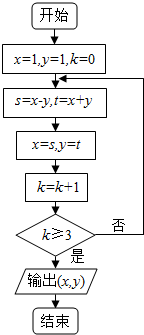

| A. | (-2,2) | B. | (-4,0) | C. | (-4,-4) | D. | (0,-8) |