题目内容
函数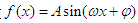 (其中
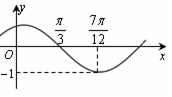
(其中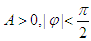 )的图象如图所示,把函数
)的图象如图所示,把函数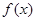 的图像向右平移
的图像向右平移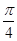 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数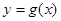 的图像.
的图像.
(1)若直线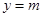 与函数
与函数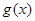 图像在
图像在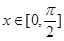 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为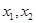 ,求
,求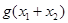 的值;
的值;
(2)已知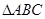 内角
内角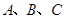 的对边分别为
的对边分别为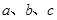 ,且
,且
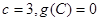 .若向量
.若向量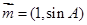 与
与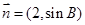 共线,求
共线,求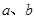 的值.
的值.
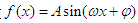 (其中
(其中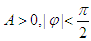 )的图象如图所示,把函数
)的图象如图所示,把函数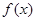 的图像向右平移
的图像向右平移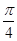 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数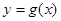 的图像.
的图像.
(1)若直线
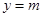 与函数
与函数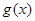 图像在
图像在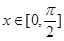 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为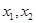 ,求
,求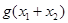 的值;
的值;(2)已知
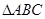 内角
内角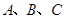 的对边分别为
的对边分别为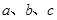 ,且
,且
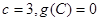 .若向量
.若向量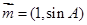 与
与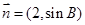 共线,求
共线,求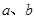 的值.
的值.(1)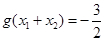 ;(2)
;(2)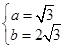
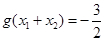 ;(2)
;(2)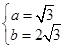
试题分析:本题主要考查三角函数的图像和性质,向量共线的充要条件以及解三角形中正弦定理余弦定理的应用,考查分析问题解决问题的能力和计算能力,考查数形结合思想和化归与转化思想.第一问,先由函数图像确定函数解析式,再通过函数图像的平移变换得到
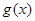 的解析式,由于
的解析式,由于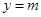 与
与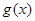 在
在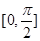 上有2个公共点,根据函数图像的对称性得到2个交点的横坐标的中点为
上有2个公共点,根据函数图像的对称性得到2个交点的横坐标的中点为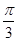 ,所以
,所以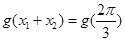 得出函数值;第二问,先用
得出函数值;第二问,先用 在
在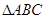 中解出角
中解出角 的值,再利用两向量共线的充要条件得到
的值,再利用两向量共线的充要条件得到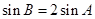 ,从而利用正弦定理得出
,从而利用正弦定理得出 ,最后利用余弦定理列出方程解出边
,最后利用余弦定理列出方程解出边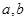 的长.
的长.试题解析:(1)由函数
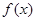 的图象,
的图象, ,得
,得 ,
,又
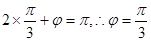 ,所以
,所以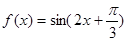 2分
2分由图像变换,得
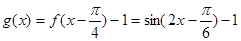 4分
4分由函数图像的对称性,有
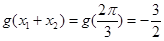 6分
6分 (Ⅱ)∵
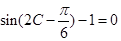 , 即
, 即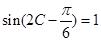
∵
 ,
,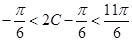 ,
,∴
 ,∴
,∴ 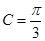 . 7分
. 7分∵
 共线,∴
共线,∴ 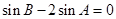 .
.由正弦定理
 , 得
, 得 ① 9分
① 9分∵
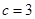 ,由余弦定理,得
,由余弦定理,得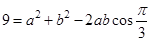 , ② 11分
, ② 11分解方程组①②,得
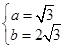 . 12分
. 12分
练习册系列答案
相关题目
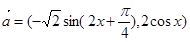 ,
,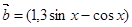 ,
,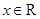 ,函数
,函数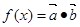 .
.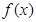 的最小正周期;
的最小正周期;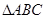 中,角
中,角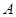 、
、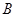 、
、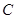 所对的边分别为
所对的边分别为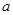 、
、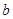 、
、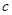 ,
,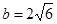 ,
,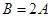 ,
,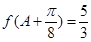 ,求
,求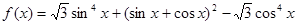 .
.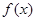 的最小值及取最小值时
的最小值及取最小值时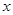 的集合;
的集合;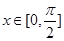 时的值域;
时的值域;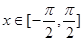 时的单调递减区间.
时的单调递减区间. .
.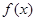 的单调减区间;
的单调减区间;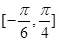 上最大值和最小值.
上最大值和最小值.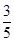 ,tan(α-β)=-
,tan(α-β)=-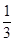 .求cosβ的值.
.求cosβ的值.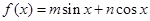 ,且
,且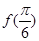 是它的最大值,(其中m、n为常数且
是它的最大值,(其中m、n为常数且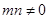 )给出下列命题:①
)给出下列命题:①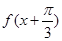 是偶函数;②函数
是偶函数;②函数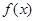 的图象关于点
的图象关于点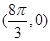 对称;③
对称;③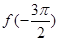 是函数
是函数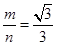 .
. sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈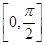 .
. 在直线
在直线 上,则
上,则 的值等于 。
的值等于 。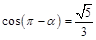 ,且
,且 ,则
,则 ( )
( )


