题目内容
已知函数f(x)= 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )
| A.(-∞,-1)∪(2,+∞) | B.(-1,2) |
| C.(-2,1) | D.(-∞,-2)∪(1,+∞) |
C
解析试题分析:当x≥0 时,f(x)=x2+4x,由二次函数的性质知,它在[0,+∞)上是增函数,当x<0时,f(x)=4x-x2,由二次函数的性质知,它在(-∞,0)上是增函数,又该函数连续,则函数f(x) 是定义在R 上的增函数,∵f(2-a2)>f(a),∴2-a2>a,解得-2<a<1,即实数a 的取值范围是(-2,1),故选C
考点:本题考查了函数的奇偶性和单调性
点评:利用单调性将不等式f(2-a2)>f(a)转化为一元二次不等式,求出实数a 的取值范围,属于中档题

练习册系列答案
相关题目
已知 , 四个函数中,当
, 四个函数中,当 时, 满足不等式
时, 满足不等式 的是
的是
A. | B. |
C. | D. |
下列函数中,在 上为增函数的是 ( )
上为增函数的是 ( )
A. | B. | C. | D. |
函数
 的部分图象如图所示,则
的部分图象如图所示,则 ( )
( )
A. | B.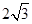 | C. | D. |
已知直线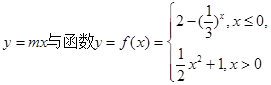 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.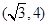 | B.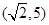 | C. | D. |
函数, 的定义域为
的定义域为
A. | B. | C. | D. |
已知函数
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,不等式
时,不等式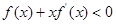 成立,若
成立,若 ,
,
 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
 (其中
(其中 )的图象如右图所示,则函数
)的图象如右图所示,则函数 的图象是( )
的图象是( )

 )的图象是( )
)的图象是( )