题目内容
求证:当一个圆和一个正方形的周长相等时,圆的面积比正方形的面积大.
证明见解析
证明:(分析法)设圆和正方形的周长为 ,依题意,圆的面积为
,依题意,圆的面积为 ,
,
正方形的面积为 .
.
因此本题只需证明 .
.
要证明上式,只需证明 ,
,
两边同乘以正数 ,得
,得 .
.
因此,只需证明 .
.
 上式是成立的,所以
上式是成立的,所以 .
.
这就证明了如果一个圆和一个正方形的周长相等,那么圆的面积比正方形的面积最大.
 ,依题意,圆的面积为
,依题意,圆的面积为 ,
,正方形的面积为
 .
.因此本题只需证明
 .
.要证明上式,只需证明
 ,
,两边同乘以正数
 ,得
,得 .
.因此,只需证明
 .
. 上式是成立的,所以
上式是成立的,所以 .
.这就证明了如果一个圆和一个正方形的周长相等,那么圆的面积比正方形的面积最大.

练习册系列答案
相关题目
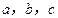 求证:
求证: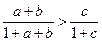
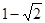 与
与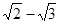
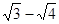
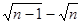 与
与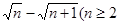 且n
且n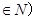 的大小,并用分析法加以证明。
的大小,并用分析法加以证明。 ,且
,且 ,则
,则 .
.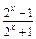 (x∈R),
(x∈R), ,则
,则
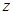 满足
满足 ,则
,则 等于( )
等于( )



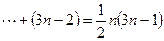 ,
,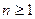
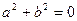 ,则
,则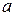 、
、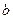 全为0(
全为0(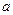 、
、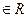 )”,其反设正确的
)”,其反设正确的