题目内容
已知命题p:指数函数f(x)=(2a-6)x在R上单调递减,命题q:关于x的方程x2-3ax+2a2+1=0的两个实根均大于3.若p或q为真,p且q为假,求实数a的取值范围.
【答案】
{a|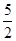 <a≤3或a≥
<a≤3或a≥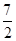 }.
}.
【解析】
试题分析:若p真,则f(x)=(2a-6)x在R上单调递减,
∴0<2a-6<1,∴3<a<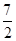 ,
,
若q真,令f(x)=x2-3ax+2a2+1,则应满足
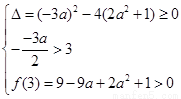 ,
,
∴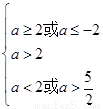 ,故a>
,故a>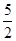 ,
,
又由题意应有p真q假或p假q真. 6分
①若p真q假,则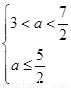 ,a无解.
,a无解.
②若p假q真,则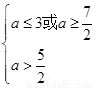 ,
,
∴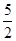 <a≤3或a≥
<a≤3或a≥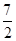 .
6分
.
6分
故a的取值范围是{a|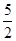 <a≤3或a≥
<a≤3或a≥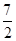 }.
14分
}.
14分
考点:指数函数的单调性;二次方程根的分布问题;复合命题真假的判断。
点评:⑴本题主要考查一个一元二次方程根的分布问题.在二次项系数不确定的情况下,一定要分二次项系数分为0和不为0两种情况讨论.
⑵设一元二次方程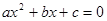 (
(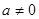 )的两个实根为
)的两个实根为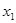 ,
,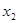 ,且
,且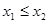 。
。
① 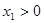 ,
,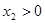 (两个正根)
(两个正根)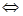
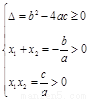 ;
;
② 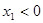 ,
,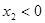 (两个负根)
(两个负根)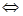
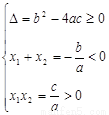 ;
;
③ 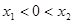 (一个正根一个负根)
(一个正根一个负根)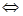
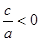 。
。

练习册系列答案
相关题目
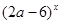 在R上单调递减; 命题q:关于x的方程
在R上单调递减; 命题q:关于x的方程 的两个实根均大于0,若
的两个实根均大于0,若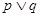 为真,
为真,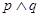 为假,求实数a的取值范围。
为假,求实数a的取值范围。