题目内容
已知命题p：指数函数y=ax在R上单调递增；命题q：函数y=x2+（a-1）x+1有两个不等的根，若p∨q为真，?q也为真．求实数a的取值范围．
分析：根据指数函数的性质可知，若p真：a＞1，若q真：△=（a-1）2-4＞0，分别求出a的范围，由题意可知q假，p真，可求
解答：解：根据指数函数的性质可知，若p真：a＞1，
若q真：△=（a-1）2-4=a2-2a-3＞0
即a＞3或a＜-1（4分）
∵p∨q为真，?q也为真
故q假，p真
∴
∴1＜a≤3（9分）
若q真：△=（a-1）2-4=a2-2a-3＞0
即a＞3或a＜-1（4分）
∵p∨q为真，?q也为真
故q假，p真
∴
|
∴1＜a≤3（9分）
点评：本题主要考查了指数函数的单调性的性质的应用，二次函数性质的应用及复合命题的真假关系的简单应用．
练习册系列答案
相关题目
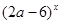在R上单调递减; 命题q：关于x的方程
的两个实根均大于0，若
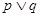为真，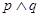
为假，求实数a的取值范围。