题目内容
已知命题p:指数函数f(x)=(2a-6)x在R上单调递减,命题q:关于x的方程x2-3ax+2a2+1=0的两个实根均大于3.若p或q为真,p且q为假,求实数a的取值范围.分析:根据指数函数的单调性求出命题p为真命题时a的范围,利用二次方程的实根分布求出命题q为真命题时a的范围;
据复合命题的真假与构成其简单命题真假的关系将“p或q为真,p且q为假”转化为p q的真假,列出不等式解得.
据复合命题的真假与构成其简单命题真假的关系将“p或q为真,p且q为假”转化为p q的真假,列出不等式解得.
解答:解:若p真,则f(x)=(2a-6)x在R上单调递减,
∴0<2a-6<1,
∴3<a<
.
若q真,令f(x)=x2-3ax+2a2+1,则应满足
∴
∴a>
,
又由题意应有p真q假或p假q真.
①若p真q假,则
,a无解.
②若p假q真,则
∴
<a≤3或a≥
.
∴0<2a-6<1,
∴3<a<
| 7 |
| 2 |
若q真,令f(x)=x2-3ax+2a2+1,则应满足
|
|
∴a>
| 5 |
| 2 |
又由题意应有p真q假或p假q真.
①若p真q假,则
|
②若p假q真,则
|
∴
| 5 |
| 2 |
| 7 |
| 2 |
点评:本题考查复合命题的真假与简单命题真假的关系;考查二次方程实根分布.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
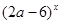 在R上单调递减; 命题q:关于x的方程
在R上单调递减; 命题q:关于x的方程 的两个实根均大于0,若
的两个实根均大于0,若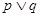 为真,
为真,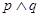 为假,求实数a的取值范围。
为假,求实数a的取值范围。