Question

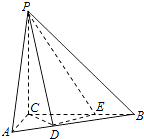
【题目】在三棱锥P﹣ABC中，底面ABC是边长为6的正三角形，PA⊥底面ABC，且PB与底面ABC所成的角为 ．
（1）求三棱锥P﹣ABC的体积；
（2）若M是BC的中点，求异面直线PM与AB所成角的大小（结果用反三角函数值表示）．

Answer 1

【答案】
（1）解：∵PA⊥平面ABC，

∴∠PBA为PB与平面ABC所成的角，即 ，

∵PA⊥平面ABC，∴PA⊥AB，又AB=6，∴ ，

∴

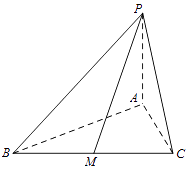
（2）解：取棱AC的中点N，连接MN，NP，

∵M，N分别是棱BC，AC的中点，

∴MN∥BA，∴∠PMN为异面直线PM与AB所成的角．

∵PA⊥平面ABC，所以PA⊥AM，PA⊥AN，

又 ，AN= AC=3，BM= BC=3，

∴AM= =3 ， ， ，

所以 ，

故异面直线PM与AB所成的角为 ．

【解析】（1）在Rt△PAB中计算PA，再代入棱锥的体积公式计算；（2）取棱AC的中点N，连接MN，NP，分别求出△PMN的三边长，利用余弦定理计算cos∠PMN即可．
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．