题目内容
已知a=(sinx,-cosx),b=(cosx,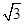 cosx),函数 f(x)=a.·b+
cosx),函数 f(x)=a.·b+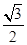 .
.
(1)求 f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当0≤x≤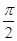 时,求函数 f(x)的值域.
时,求函数 f(x)的值域.
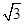 cosx),函数 f(x)=a.·b+
cosx),函数 f(x)=a.·b+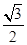 .
.(1)求 f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当0≤x≤
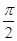 时,求函数 f(x)的值域.
时,求函数 f(x)的值域.解:(1) f(x)=sinxcosx-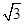 cos2x+
cos2x+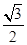
=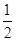 sin2x-
sin2x-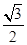 (cos2x+1)+
(cos2x+1)+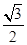 =
=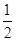 sin2x-
sin2x-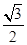 cos2x=sin(2x-
cos2x=sin(2x-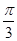 ),
),
所以 f(x)的最小正周期为π.
令sin(2x-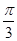 )=0,得2x-
)=0,得2x-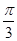 =kπ,∴x=
=kπ,∴x=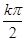 +
+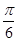 ,k∈Z.
,k∈Z.
故所求对称中心的坐标为(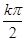 +
+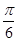 ,0)(k∈Z).
,0)(k∈Z).
(2)∵0≤x≤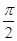 ,∴-
,∴-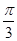 ≤2x-
≤2x-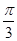 ≤
≤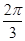 .
.
∴-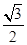 ≤sin(2x-
≤sin(2x-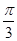 )≤1,
)≤1,
即 f(x)的值域为[-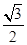 ,1].
,1].
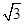 cos2x+
cos2x+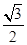
=
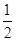 sin2x-
sin2x-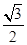 (cos2x+1)+
(cos2x+1)+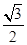 =
=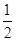 sin2x-
sin2x-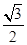 cos2x=sin(2x-
cos2x=sin(2x-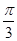 ),
),所以 f(x)的最小正周期为π.
令sin(2x-
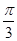 )=0,得2x-
)=0,得2x-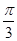 =kπ,∴x=
=kπ,∴x=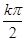 +
+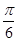 ,k∈Z.
,k∈Z.故所求对称中心的坐标为(
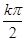 +
+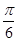 ,0)(k∈Z).
,0)(k∈Z).(2)∵0≤x≤
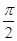 ,∴-
,∴-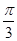 ≤2x-
≤2x-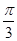 ≤
≤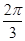 .
.∴-
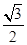 ≤sin(2x-
≤sin(2x-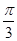 )≤1,
)≤1,即 f(x)的值域为[-
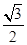 ,1].
,1].略

练习册系列答案
相关题目
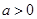 ,函数
,函数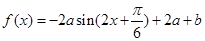 ,当
,当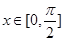 时,
时,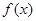 的值域为
的值域为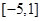 .
.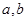 的值;
的值;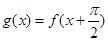 ,
,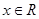 ,求
,求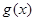 的单调区间.
的单调区间.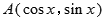 ,
,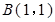 ,
,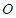 为坐标原点,
为坐标原点,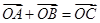 ,
,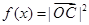 .(Ⅰ)求
.(Ⅰ)求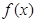 的对称中心的坐标及单调递减区间;
的对称中心的坐标及单调递减区间;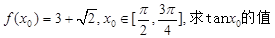 .
.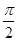 ,直线x=
,直线x= 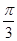 是其图象的一条对称轴,则它的解析式是( )
是其图象的一条对称轴,则它的解析式是( )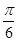 )
)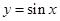 的图象上每点的横坐标缩小为原来的
的图象上每点的横坐标缩小为原来的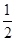 (纵坐标不变),再把所得图象向左平移
(纵坐标不变),再把所得图象向左平移 个单位,得到的函数解析式为( )
个单位,得到的函数解析式为( )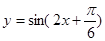
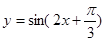
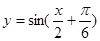
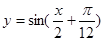
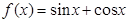 ,设
,设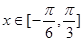 ,若
,若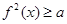 恒成立,则实数
恒成立,则实数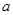 的取值范围为_______.
的取值范围为_______.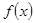 是以2为周期的奇函数,若
是以2为周期的奇函数,若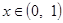 时,
时,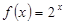 ,则
,则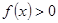
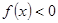
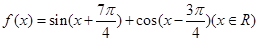 。
。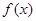 的对称轴;
的对称轴;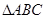 中,已知
中,已知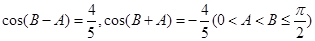 ,求
,求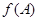 。
。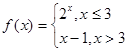 ,则
,则 =
=