Question

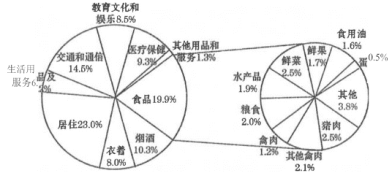
【题目】如图，在多面体ABCDEF中，四边形ABCD是矩形，四边形ABEF为等腰梯形，且，平面ABCD⊥平面ABEF

（1）求证：BE⊥DF；

（2）求三棱锥C﹣AEF的体积V．

Answer 1

【答案】（1）见解析； （2）.

【解析】

（1）取的中点，连结，则，利用勾股定理可得，由面面垂直的性质可得 平面，可得，由此可得 平面，则 平面，从而可得结果；（2）平面，可得，由（1）得， 平面，由棱锥的体积公式可得结果.

（1）取EF的中点G，连结AG，

∵EF=2AB，∴AB=EG，

又AB∥EG，∴四边形ABEG为平行四边形，

∴AG∥BE，且AG=BE=AF=2，

在△AGF中，GF=，AG=AF=2，

∴，∴AG⊥AF，

∵四边形ABCD是矩形，∴AD⊥AB，

又平面ABCD⊥平面ABEF，且平面ABCD平面ABEF=AB，

∴AD⊥平面ABEF，又AG平面ABEF，

∴AD⊥AG，

∵ADAF=A，∴AG⊥平面ADF，

∵AG∥BE，∴BE⊥平面ADF，

∵DF平面ADF，∴BE⊥DF；

（2）∵CD∥AB且平面ABEF，BA平面ABEF，

∴CD∥平面ABEF，∴，

由（1）得，DA⊥平面ABEF，

∵，∴．