题目内容
已知曲线C：y=
与直线l：y=2x+k，当k为何值时，l与C：①有一个公共点；②有两个公共点；③没有公共点．
| 1-x2 |
分析：先画出函数的图象，再根据图象可得结论．
解答：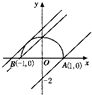
解：曲线C：y=
（|x|≤1）．如图所示，
若直线l与曲线C相切，则
=1，所以k=±
（舍去负值）；
若直线l过点A（1，0），则0=2•1+k，所以k=-2；
若直线l过点B（-1，0），则0=2•（-1）+k，所以k=2．
结合图可知，
①当-2≤k＜2或k=
时，l与C有一个公共点；
②当2≤k＜
时，l与C有两个公共点；
③当k＜-2或k＞
时，l与C无公共点．
解：曲线C：y=| 1-x2 |
若直线l与曲线C相切，则
| |k| | ||
|
| 5 |
若直线l过点A（1，0），则0=2•1+k，所以k=-2；
若直线l过点B（-1，0），则0=2•（-1）+k，所以k=2．
结合图可知，
①当-2≤k＜2或k=
| 5 |
②当2≤k＜
| 5 |
③当k＜-2或k＞
| 5 |
点评：本题重点考查直线与曲线的交点，解题的关键是利用数形结合，利用特殊位置确定k的值，属于中档题．
练习册系列答案
相关题目
如图，已知曲线
已知曲线C：y=
x3-x2-4x+1，直线l：x+y+2k-1=0，当x∈[-3，3]时，直线l 恒在曲线C的上方，则实数k的取值范围是（ ）
| 1 |
| 3 |
A、k＞-
| ||
B、k＜-
| ||
C、K＜
| ||
D、K＞
|