题目内容
18．已知$\overrightarrow{a}$=（cos40°，sin40°），$\overrightarrow{b}$=（cos80°，-sin80°），则$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）| A． | 1 | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
分析 由平面向量的数量积公式，可得$\overrightarrow{a}$•$\overrightarrow{b}$=cos40°•cos80°-sin40°•sin80°，再由两角和的余弦公式，可得答案．
解答 解：∵$\overrightarrow{a}$=（cos40°，sin40°），$\overrightarrow{b}$=（cos80°，-sin80°），
∴$\overrightarrow{a}$•$\overrightarrow{b}$=cos40°•cos80°-sin40°•sin80°=cos（40°+80°）=cos120°=-$\frac{1}{2}$，
故选：C
点评 本题考查的知识点是两角和与差的余弦公式，平面向量的数量积公式，难度不大，属于基础题．
练习册系列答案
相关题目
10．
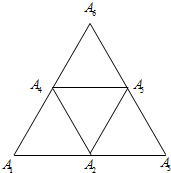如图，由四个边长为1的等边三角形拼成一个边长为2的等边三角形，各项点依次为，A1，A2，A3，…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}}，（{i，j∈[{1，2，3，…6}]}）$的值组成的集合为（ ）
如图，由四个边长为1的等边三角形拼成一个边长为2的等边三角形，各项点依次为，A1，A2，A3，…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}}，（{i，j∈[{1，2，3，…6}]}）$的值组成的集合为（ ）| A． | {-2，-1，0，1，2} | B． | $\left\{{-2，-1，-\frac{1}{2}，0，\frac{1}{2}，1，2}\right\}$ | ||
| C． | $\left\{{-\frac{3}{2}，-1，-\frac{1}{2}，0，\frac{1}{2}，1，\frac{3}{2}}\right\}$ | D． | $\left\{{-2，-\frac{3}{2}，-1，-\frac{1}{2}，0，\frac{1}{2}，1，\frac{3}{2}，2}\right\}$ |