Question

设函数f（x）=x³+3bx²+3cx在两个极值点x₁、x₂，且x₁∈[-1，0]，x₂∈[1，2]．
（1）求b、c满足的约束条件，并在下面的坐标平面内，画出满足这些条件的点（b，c）的区域；
（2）证明：-10≤f(x2)≤-

1

2

Answer 1

（Ⅰ）f'（x）=3x²+6bx+3c，（2分）
依题意知，方程f'（x）=0有两个根x₁、x₂，且x₁∈[-1，0]，x₂∈[1，2]
等价于f'（-1）≥0，f'（0）≤0，f'（1）≤0，f'（2）≥0．
由此得b，c满足的约束条件为

c≥2b-1 c≤0 c≤-2b-1 c≥-4b-4

（4分）
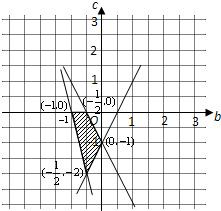
满足这些条件的点（b，c）的区域为图中阴影部分．（6分）

（Ⅱ）由题设知f'（x₂）=3x₂²+6bx₂+3c=0，
则bx2=-

1

2

x

22

-

1

2

c，
故f(x2)=

x

32

+3b

x

22

+3cx2=-

1

2

x

32

+

3c

2

x2．（8分）
由于x₂∈[1，2]，而由（Ⅰ）知c≤0，
故-4+3c≤f(x2)≤-

1

2

+

3

2

c．
又由（Ⅰ）知-2≤c≤0，（10分）
所以-10≤f(x2)≤-

1

2

．