Question

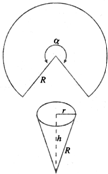
用半径为R的圆形铁皮剪出一个圆心角为α的扇形，制成一个圆锥形容器，求：扇形的圆心角多大时，容器的容积最大？并求出此时容器的最大容积．

Answer 1

设圆锥的底面半径为r，高为h，体积为V，那么r²+h²=R²，
因此，V=

1

3

πr2h
=

1

3

π(R2-h2)h=

1

3

πR2h-

1

3

πh3(0＜h＜R)．…（3分）
V′=

1

3

πR2-πh2．
令V'=0，即

1

3

πR2-πh2=0，得 h=

3

3

R．…（5分）
当 0＜h＜

3

3

R时，V'＞0．
当

3

3

R＜h＜R时，V'＜0．
所以，h=

3

3

R时，V取得极大值，并且这个极大值是最大值．…（8分）
把 h=

3

3

R代入r²+h²=R²，得 r=

6

3

R．
由Rα=2πr，得 α=

2 6

3

π
答：圆心角α为

2 6

3

π弧度时，漏斗容积最大．…（12分）