题目内容
17.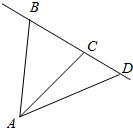 如图,设A,B,C是不共线的三点,$\overrightarrow{AB}=\overrightarrow p,\overrightarrow{AC}=\overrightarrow q$,若点D在线段BC上,且BC:CD=5:2,则向量$\overrightarrow{AD}$=$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$(用向量$\overrightarrow p,\overrightarrow q$表示).
如图,设A,B,C是不共线的三点,$\overrightarrow{AB}=\overrightarrow p,\overrightarrow{AC}=\overrightarrow q$,若点D在线段BC上,且BC:CD=5:2,则向量$\overrightarrow{AD}$=$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$(用向量$\overrightarrow p,\overrightarrow q$表示).
分析 由BC:CD=5:2,可得$BD=\frac{7}{5}BC$.再利用向量三角形法则与向量共线定理即可得出.
解答 解:∵BC:CD=5:2,
∴$BD=\frac{7}{5}BC$.
$\overrightarrow{AD}=\overrightarrow{BD}-\overrightarrow{BA}$=$\frac{7}{5}\overrightarrow{BC}+\overrightarrow{AB}$=$\frac{7}{5}(\overrightarrow{AC}-\overrightarrow{AB})+\overrightarrow{AB}$=$\frac{7}{5}\overrightarrow{AC}-\frac{2}{5}\overrightarrow{AB}$=$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$.
故答案为:$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$.
点评 本题考查了向量三角形法则与向量共线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知四个函数y=3x,y=x2,y=3x,y=log3x,其中奇函数是( )
| A. | y=3x | B. | y=x2 | C. | y=3x | D. | y=log3x |
7.已知函数$f(x+\frac{π}{2})$为偶函数,当$x∈(-\frac{π}{2},\frac{π}{2})$时,f(x)=x3+sinx,若a=f(1),b=f(2),c=f(3),则有( )
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |