题目内容
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为ξ,求ξ的分布列和数学期望.
解:(1)设“这箱产品被用户接收”为事件A,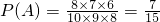
即这箱产品被用户接收的概率为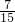 .
.
(2)ξ的可能取值为1,2,3.
P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)= ×
× =
= ,P(ξ=3)=
,P(ξ=3)=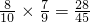 ,
,
∴ξ的概率分布列为:
∴Eξ=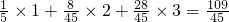 .
.
分析:由题设每次抽取到什么产品是独立的,可用 乘法公式求解,
(1)这箱产品被用户接收,即前三次没有抽取到次品,根据乘法公式求出概率;
(2)由题意抽检的产品件数为ξ的值为0,1,2,3,故计算出P(ξ=i)(i=1,2,3)的概率,列出分布列,由公式求出数学期望即可.
点评:本题考查离散型随机变量及其分布列,考查作出分布列的方法以及根据分布列求出变量的期望的能力,解答本题的关键是分清事件的结构.
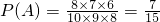
即这箱产品被用户接收的概率为
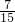 .
. (2)ξ的可能取值为1,2,3.
P(ξ=1)=
 ,P(ξ=2)=
,P(ξ=2)= ×
× =
= ,P(ξ=3)=
,P(ξ=3)=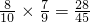 ,
,∴ξ的概率分布列为:
| ξ | 1 | 2 | 3 | |
| P |  |  |  |
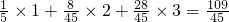 .
.分析:由题设每次抽取到什么产品是独立的,可用 乘法公式求解,
(1)这箱产品被用户接收,即前三次没有抽取到次品,根据乘法公式求出概率;
(2)由题意抽检的产品件数为ξ的值为0,1,2,3,故计算出P(ξ=i)(i=1,2,3)的概率,列出分布列,由公式求出数学期望即可.
点评:本题考查离散型随机变量及其分布列,考查作出分布列的方法以及根据分布列求出变量的期望的能力,解答本题的关键是分清事件的结构.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目