题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)因为![]() ,
,![]() ,可得
,可得![]() ,分别讨论
,分别讨论![]() ,
,![]() 和
和![]() 函数
函数![]() 的单调性,即可求得答案;
的单调性,即可求得答案;
(2)求得函数![]() 在区间
在区间![]() 的最小值
的最小值![]() ,构造函数
,构造函数![]() (
(![]() ),求其最值,即可求得答案.
),求其最值,即可求得答案.
![]()
![]() ,
,![]() .
.
![]()
①当![]()
![]()
当![]() ,即
,即![]() ,
,![]()
此时![]() 在
在![]() 是单调递增
是单调递增
当![]() ,即
,即![]() ,
,![]()
此时![]() 在
在![]() 是单调递减
是单调递减
②当![]()
![]()
ⅰ.当![]() 时,即
时,即![]() ,不符题意;
,不符题意;
ⅱ.当![]() 时,即
时,即![]() ,不符题意;
,不符题意;
ⅲ. 当![]() 时,即
时,即![]() ,故
,故![]()
由![]() ,解得
,解得![]() ,
,![]()
则当![]() 或
或![]() ,
,![]() ,此时
,此时![]() 是单调递增;
是单调递增;
当![]() ,
,![]() ,此时
,此时![]() 是单调递减.
是单调递减.
③当![]()
![]()
ⅰ.当![]() 时,即
时,即![]()
则![]() 在
在![]() 恒成立,此时
恒成立,此时![]() 是单调递减
是单调递减
ⅱ.当![]() 时,即
时,即![]() ,
,
则![]() 在
在![]() 恒成立,当且仅当
恒成立,当且仅当![]() 等号成立
等号成立
此时此时![]() 在
在![]() 是单调递减
是单调递减
ⅲ. 当![]() 时,即
时,即![]()
故![]()
由![]() ,解得
,解得![]() ,
,![]()
则当![]() 或
或![]() ,
,![]() ,此时
,此时![]() 是单调递减;
是单调递减;
当![]() ,
,![]() ,此时
,此时![]() 是单调递增.
是单调递增.
(2)当![]() 时,
时,![]()
![]()
![]()
则当![]() 或
或![]() ,
,![]() ,此时
,此时![]() 是单调递增;
是单调递增;
当![]() ,
,![]() ,此时
,此时![]() 是单调递减.
是单调递减.
![]() 函数
函数![]() 在区间
在区间![]() 上,
上,
当![]() ,
,![]() 单调递减.
单调递减.
当![]() ,
,![]() 单调递增.
单调递增.
![]() 当
当![]() ,
,![]() 取得最小值,
取得最小值,![]()
令![]() ,(
,(![]() )
)
即![]()
可得:![]() (
(![]() )
)
![]()
![]()
![]()
当![]() ,
,![]() ,可得
,可得![]() 单调递减;
单调递减;
当![]() ,
,![]() ,可得
,可得![]() 单调递增;
单调递增;
![]() 当
当![]() 时,
时,![]() 取的最小值,
取的最小值,![]()
故![]()
![]()
![]()
故![]()

 导学全程练创优训练系列答案
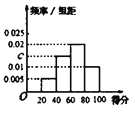
导学全程练创优训练系列答案【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变,在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险的基准保费为a元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况相联系,最终保费![]() 基准保费
基准保费![]() (
(![]() 与道路交通事故相联系的浮动比率),具体情况如下表:
与道路交通事故相联系的浮动比率),具体情况如下表:
交强险浮动因素和浮动费率比率表 | ||
类别 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
为了解某一品牌普通6座以下私家车的投保情况,随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
类型 |
|
|
|
|
|
|
数量 | 20 | 10 | 10 | 38 | 20 | 2 |
若以这100辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
A.a元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元