题目内容
已知抛物线y2=2px,O是坐标原点,F是焦点,P是抛物线上的点,使得△POF是直角三角形,则这样的点P共有( )
分析:如图所示,过焦点F作PF⊥x轴,交抛物线于点P,P′.则△OFP、△OFP′都是直角三角形.而tan∠POF=
=
=2>1,可得∠POF>45°.即∠POP′>90°.于是△POP′不是直角三角形.即可得出符合条件的点P的个数.
| PF |
| OF |
| p | ||
|
解答:解:如图所示,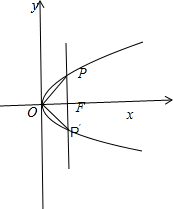
过焦点F作PF⊥x轴,交抛物线于点P,P′.则△OFP、△OFP′都是直角三角形.
而tan∠POF=
=
=2>1,∴∠POF>45°.∴∠POP′>90°.
∴△POP′不是直角三角形.
综上可知:使得△POF是直角三角形的抛物线上的点P有且只有2个.
故选B.

过焦点F作PF⊥x轴,交抛物线于点P,P′.则△OFP、△OFP′都是直角三角形.
而tan∠POF=
| PF |
| OF |
| p | ||
|
∴△POP′不是直角三角形.
综上可知:使得△POF是直角三角形的抛物线上的点P有且只有2个.
故选B.
点评:本题考查了抛物线的性质、直角三角形,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目