题目内容
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点分别为F1、F2,点M是双曲线右支上一点,且MF1⊥MF2,延长MF2交双曲线C于点P,若|MF1|=|PF2|,则双曲线C的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{10}}{2}$ | D. | $\sqrt{6}$ |
分析 设|MF1|=t,由双曲线的定义可得|MF2|=t-2a,|PF2|=t,|PF1|=t+2a,再由勾股定理,求得t=3a,及a,c的关系,运用离心率公式即可得到所求.
解答  解:设|MF1|=t,由双曲线的定义可得|MF2|=t-2a,
解:设|MF1|=t,由双曲线的定义可得|MF2|=t-2a,
|PF2|=t,|PF1|=t+2a,
由MF1⊥MF2,可得|MF1|2+|MP|2=|PF1|2,
即t2+(2t-2a)2=(t+2a)2,
解得t=3a,
又|MF1|2+|MF2|2=|F2F1|2,
即为(3a)2+a2=4c2,
即为c=$\frac{\sqrt{10}}{2}$a,
则e=$\frac{c}{a}$=$\frac{\sqrt{10}}{2}$.
故选:C.
点评 本题考查双曲线的定义、方程和性质,主要考查离心率的求法,注意两次运用勾股定理,属于中档题.

练习册系列答案
相关题目
13.已知f(x)=$\left\{\begin{array}{l}{1-x-2{x}^{2}}&{x≤0}\\{|lgx|}&{x>0}\end{array}\right.$若关于x的方程f(x)=a有四个实根x1,x2,x3,x4,则这四根之积x1,x2,x3,x4的取值范围是( )
| A. | [0,$\frac{1}{2}$) | B. | [0,$\frac{1}{4}$) | C. | [0,$\frac{1}{8}$) | D. | [0,$\frac{1}{16}$) |
 如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.
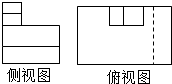
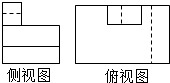
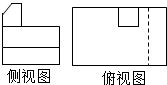
如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$. 如图所示是一位同学画的一个实物的三视图,老师判断正视图是正确的,其他两个视图有错误,则正确的侧视图和俯视图是( )
如图所示是一位同学画的一个实物的三视图,老师判断正视图是正确的,其他两个视图有错误,则正确的侧视图和俯视图是( )