题目内容
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)  .(Ⅱ)
.(Ⅱ)  .(Ⅲ)
.(Ⅲ) 的分布列为:
的分布列为:
0 1 2 3 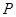




 的数学期望
的数学期望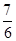 .
.
解析试题分析:(Ⅰ)设“从甲盒内取出的2个球均为黑球”为事件 ,
,
“从乙盒内取出的2个球均为黑球”为事件 .
.
由于事件 相互独立,且
相互独立,且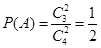 ,
, . 2分
. 2分
故取出的4个球均为黑球的概率为 . 4分
. 4分
(Ⅱ) 设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件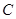 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件 .则
.则  ,
, . 6分
. 6分
由于事件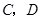 互斥,故取出的4个球中恰有1个红球的概率为
互斥,故取出的4个球中恰有1个红球的概率为 . 8分
. 8分
(Ⅲ) 可能的取值为
可能的取值为 .
.
由(Ⅰ),(Ⅱ)得 ,
, ,
, 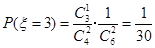 .
.
从而 .
. 的分布列为:
的分布列为:
0 1 2 3 




10分 的数学期望
的数学期望 . 12分
. 12分
考点:本题考查了随机变量的概率、分布列及期望
点评:本题考查了随机事件的概率及随机变量的分布列、期望的综合运用,考查了学生的计算能力及解决实际问题的能力,掌握求分布列的步骤及期望公式是解决此类问题的关键

哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的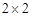 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为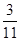 。
。
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
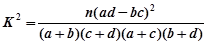 。
。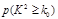 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
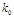 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
为了参加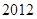 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三(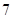 )班 )班 | 高三(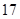 )班 )班 | 高二(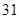 )班 )班 | 高二(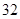 )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
(Ⅱ)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为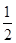 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
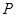 | 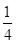 |  | 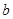 | 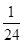 |
(2) 求
 ,
, 的值;
的值;(3) 求
 的数学期望.
的数学期望. 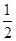 和
和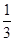 , 求:
, 求: 道备选题中一次性随机抽取
道备选题中一次性随机抽取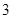 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中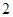 道题的便可通过.已知
道题的便可通过.已知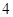 道题能正确完成,
道题能正确完成, ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.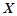 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
. 的分布列及其数学期望.
的分布列及其数学期望.