题目内容
在正三棱锥P-ABC中,M、N分别是侧棱PB,PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧面与底面所成的角的正切值是
.
| 5 |
| 5 |
分析:先作出二面角的平面角,即取BC中点D,可证明∠ADP就是侧面与底面所成的二面角的平面角,再利用截面AMN⊥侧面PBC的特点,证明△PAD是等腰三角形,从而沟通了侧棱长和底面边长间的关系,最后在直角三角形中计算tan∠ADO即可
解答: 解:如图,取MN中点O,连接AO,PO,延长PO交BC于点D,连接
解:如图,取MN中点O,连接AO,PO,延长PO交BC于点D,连接
AD,则BD=DC
∵三棱锥P-ABC为正三棱锥
∴AM=AN
∴AO⊥MN
∵截面AMN⊥侧面PBC
∴AO⊥侧面PBC
∴AO⊥PD,又PO=OD
∴PA=AD,且∠ADO就是侧面与底面所成的二面角的平面角
设AB=a,则AD=
a=PA
∵PD=
=
a
∴OD=
a∴AO=
=
a
在Rt△AOD中,tan∠ADO=
=
=
∴三棱锥的侧面与底面所成的角的正切值是
故答案为
 解:如图,取MN中点O,连接AO,PO,延长PO交BC于点D,连接
解:如图,取MN中点O,连接AO,PO,延长PO交BC于点D,连接AD,则BD=DC
∵三棱锥P-ABC为正三棱锥
∴AM=AN
∴AO⊥MN
∵截面AMN⊥侧面PBC
∴AO⊥侧面PBC
∴AO⊥PD,又PO=OD
∴PA=AD,且∠ADO就是侧面与底面所成的二面角的平面角
设AB=a,则AD=
| ||
| 2 |
∵PD=
(
|
| ||
| 2 |
∴OD=
| ||
| 4 |
(
|
| ||
| 4 |
在Rt△AOD中,tan∠ADO=
| AO |
| OD |
| ||||
|
| 5 |
∴三棱锥的侧面与底面所成的角的正切值是
| 5 |
故答案为
| 5 |
点评:本题考查了正三棱锥的性质,二面角的求法和面面垂直的性质,解题时要有空间想象力,要能恰当的沟通未知量之间的关系,能够用转化的思想方法将空间问题化为平面问题

练习册系列答案
相关题目
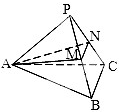 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|