题目内容
如图1,
在直角梯形 中,
中,  ,
,  ,
, ,
, 为线段
为线段 的中点. 将
的中点. 将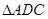 沿
沿 折起,使平面
折起,使平面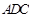
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(1)求证: 平面
平面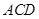 ;
;
(2)求二面角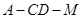 的余弦值.
的余弦值. 
【答案】
(1)根据线面垂直的性质定理来证明线线垂直。
(2)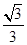
【解析】
试题分析:解析:(1)在图1中, 可得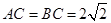 , 从而
, 从而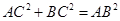 ,
,
故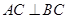 .
.
取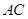 中点
中点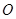 连结
连结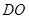 , 则
, 则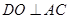 , 又面
, 又面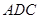
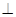 面
面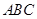 ,
,
面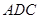
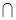 面
面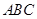
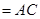 ,
, 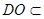 面
面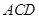 , 从而
, 从而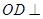 平面
平面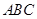 .
.
∴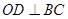 ,又
,又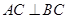 ,
,  .
.
∴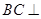 平面
平面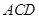 .
.
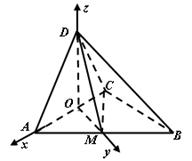
(2)建立空间直角坐标系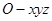 如图所示,
如图所示,
则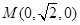 ,
, 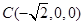 ,
, 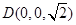 ,
,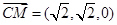 ,
,
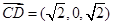 .
.
设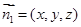 为面
为面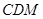 的法向量,则
的法向量,则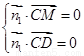 即
即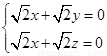 , 解得
, 解得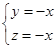 . 令
. 令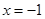 , 可得
, 可得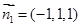 .
.
又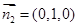 为面
为面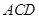 的一个法向量,∴
的一个法向量,∴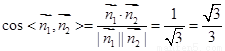 .
.
∴二面角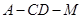 的余弦值为
的余弦值为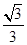 .
.
(法二)如图,取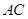 的中点
的中点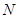 ,
,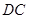 的中点
的中点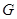 ,连结
,连结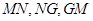 .
.
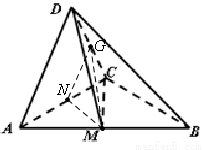
易知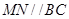 ,又
,又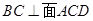 ,
,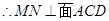 ,又
,又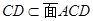 ,
,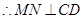 .
.
又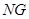 为
为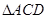 的中位线,因
的中位线,因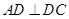 ,
,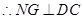 ,
,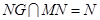 ,且
,且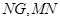 都在面
都在面 内,故
内,故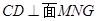 ,故
,故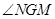 即为二面角
即为二面角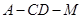 的平面角.
的平面角.
在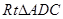 中,易知
中,易知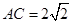 ;
;
在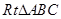 中,易知
中,易知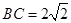 ,
,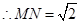 .
.
在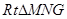 中
中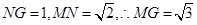 .
.
故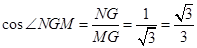 .
.
∴二面角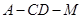 的余弦值为
的余弦值为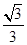 .
.
考点:棱锥中的垂直以及二面角的平面角
点评:主要是考查了运用向量法来空间中的角以及垂直的证明,属于基础题。

练习册系列答案
相关题目
 如图1,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF⊥平面ABCD,连接部分线段后围成一个空间几何体,如图2.
如图1,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF⊥平面ABCD,连接部分线段后围成一个空间几何体,如图2.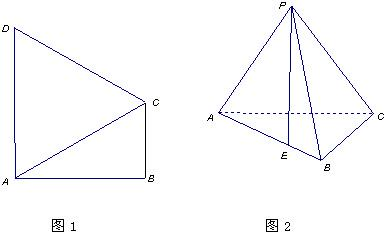 如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=1,AD=CD,把△DAC沿对角线AC折起后如图2所示(点D记为点P),点P在平面ABC上的正投影E落在线段AB上,连接PB.
如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=1,AD=CD,把△DAC沿对角线AC折起后如图2所示(点D记为点P),点P在平面ABC上的正投影E落在线段AB上,连接PB. 如图1,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
如图1,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=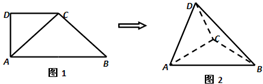 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=2,AD=CD=1.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.求几何体D-ABC的体积.
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=2,AD=CD=1.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.求几何体D-ABC的体积.