题目内容
20.若方程x2-3x+m=0在[0,2]上有两个不等实根,则实数m的取值范围是[2,$\frac{9}{4}$).分析 利用方程对应的二次函数的零点与判别式、对称轴及区间端点处的函数值的关系即可得出.
解答 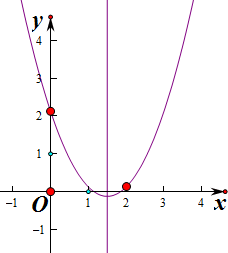 解:令f(x)=x2-3x+m,
解:令f(x)=x2-3x+m,
∵方程x2-3x+m=0在[0,2]上有两个不等实根,
∴m满足$\left\{\begin{array}{l}f(\frac{3}{2})<0\\ f(2)≥0\end{array}\right.$,即:$\left\{\begin{array}{l}\frac{9}{4}-3×\frac{3}{2}+m<0\\ 4-6+m≥0\end{array}\right.$,解得2$≤m<\frac{9}{4}$,
∴实数m的取值范围是[2,$\frac{9}{4}$).
故答案为:[2,$\frac{9}{4}$).
点评 熟练掌握二次函数的图象与性质是解题的关键.考查转化思想的应用.

练习册系列答案
相关题目
12.已知sinα+cosα=$\sqrt{2}$,α∈(0,$\frac{π}{2}$),则tanα=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
9.若集合A={x|x2-7x<0,x∈N*},则B={y|$\frac{6}{y}$∈N*,y∈A}中元素的个数为( )
| A. | 3个 | B. | 4个 | C. | 1个 | D. | 2个 |




