题目内容
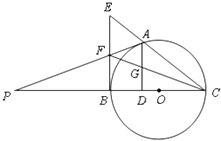
【题目】如图，在△ABC中，已知|AB|＝4 
，且三内角A，B，C满足2sin A＋sin C＝2sin B，建立适当的坐标系，求顶点C的轨迹方程．
【答案】
【解析】试题分析：先根据条件建立直角坐标系，根据正弦定理将角的关系转化为边的关系，再利用双曲线定义确定轨迹，并根据基本量求轨迹方程
试题解析：解：以AB边所在直线为x轴，AB的垂直平分线为y轴，建立平面直角坐标系(如图所示)．
则A(－2
，0)，B(2，0)．设边BC、AC、AB的长分别为a、b、c，由正弦定理得sin A＝
，sin B＝
，sin C＝
(R为△ABC外接圆的半径)．
∵2sin A＋sin C＝2sin B，∴2a＋c＝2b，即b－a＝
.
从而有|CA|－|CB|＝
|AB|＝2 <|AB|.
由双曲线的定义知，点C的轨迹为双曲线的右支(除去与x轴的交点)．∵a＝，c＝2，∴b2＝6.
∴顶点C的轨迹方程为
－
＝1(x>)．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案【题目】双“十一”结束之后，某网站针对购物情况进行了调查，参与调查的人主要集中在[20，50]岁之间，若规定：购物600（含600元）以下者，称为“理智购物”，购物超过600元者被网友形象的称为“剁手党”，得到如下统计表：
分组编号 | 年龄分组 | 球迷 | 所占比例 |
1 | [20，25） | 1000 | 0.5 |
2 | [25，30） | 1800 | 0.6 |
3 | [30，35） | 1200 | 0.5 |
4 | [35，40） | a | 0.4 |
5 | [40，45） | 300 | 0.2 |
6 | [45，50] | 200 | 0.1 |
若参与调查的“理智购物”总人数为7720人．
（1）求a的值；
（2）从年龄在[20，35）的“剁手党”中按照年龄区间分层抽样的方法抽取20人； ①从这20人中随机抽取2人，求这2人恰好属于同一年龄区间的概率；
②从这20人中随机抽取2人，用ζ表示年龄在[20，25）之间的人数，求ξ的分布列及期望值．
