题目内容
1.已知数列{an}的前n项和为Sn,且2Sn=nan+n(n=1,2,3,…),等比数列{bn}中,b1=a1,且b2,b3的等差中项为b1.(1)求证:数列{an}为等差数列.
(2)请选择一个符合已知条件的且满足a1≠a2的数列{an},并求数列{an•bn}的前n项和Tn.
分析 (1)由n=1可得a1=S1,由条件可得a1=1,再将n换为n-1,相减,运用等差数列的性质,即可得证;
(2)取a2=2,则d=1,即有an=n,由等差数列的性质和等比数列的通项,可得公比q=1或-2,再由错位相减法和等比数列的求和公式,计算即可得到所求.
解答 (1)证明:由n=1可得a1=S1,
2S1=a1+1,可得a1=1,
2Sn=nan+n,可得2Sn-1=(n-1)an-1+n-1,(n≥2),
相减可得,2an=nan-(n-1)an-1+1,
即有(n-2)an=(n-1)an-1-1,
再将n换为n-1可得(n-3)an-1=(n-2)an-2-1,
上面两式相减可得,(n-2)an+(n-2)an-2=2(n-2)an-1,
即为an+an-2=2an-1,(n>2),
即有an-an-1=d(d为常数),
故数列{an}为等差数列;
(2)解:可取a2=2,则d=1,
即有an=n,
由b1=a1,且b2,b3的等差中项为b1.
可得2b1=b2+b3,即为2=q+q2,(q为公比),
解得q=-2或1.
当q=1时,bn=1,
前n项和Tn=$\frac{1}{2}$n(n+1);
当q=-2,即有Tn=1•(-2)0+2•(-2)+3•(-2)2+…+n•(-2)n-1,
-2Tn=1•(-2)+2•(-2)2+3•(-2)3+…+n•(-2)n,
两式相减可得,3Tn=1+(-2)+(-2)2+…+(-2)n-1-n•(-2)n
=$\frac{1-(-2)^{n}}{1-(-2)}$-n•(-2)n,
化简可得,Tn=$\frac{1-(1+3n)•(-2)^{n}}{9}$.
点评 本题考查数列的通项和求和之间的关系,考查等差数列的定义和通项和求和公式的运用,同时考查等比数列的求和公式的运用,以及错位相减法求和,属于中档题.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | 所有的直角三角形 | B. | 圆x2+y2=1上的所有点 | ||
| C. | 高一年级中家离学校很远的学生 | D. | 高一年级的班主任 |
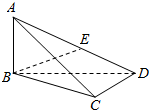 四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD,且AB=BC=6,BD=8,E是AD中点,求BE与CD所成角的余弦值.
四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD,且AB=BC=6,BD=8,E是AD中点,求BE与CD所成角的余弦值.