题目内容
（2012•盐城一模）已知四边形ABCD为梯形，AB∥CD，l为空间一直线，则“l垂直于两腰AD，BC”是“l垂直于两底AB，DC”的
充分不必要
充分不必要
条件（填写“充分不必要”，“必要不充分”，“充要”，“既不充分也不必要”中的一个）．分析：先看充分性，当l垂直于两腰AD，BC时，根据直线与平面垂直的判定定理，可得l与平面ABCD垂直，结合AB，DC是平面ABCD内的直线，得到l垂直于两底AB，DC，充分性成立；
再看必要性，作出梯形ABCD的高AE，设AE所在直线为l，可得l满足垂直于两底AB，DC，但是l不与梯形ABCD的两腰垂直，必要性不成立．由此得到正确答案．
再看必要性，作出梯形ABCD的高AE，设AE所在直线为l，可得l满足垂直于两底AB，DC，但是l不与梯形ABCD的两腰垂直，必要性不成立．由此得到正确答案．
解答：解：先看充分性
∵四边形ABCD为梯形，AB∥CD，
∴两腰BC、AD所在直线是相交直线．
∵l垂直于两腰AD，BC
∴l⊥平面ABCD
又∵AB，DC是平面ABCD内的直线，
∴l垂直于两底AB，DC，因此充分性成立；
再看必要性
作出梯形ABCD的高AE，则AE垂直于两底AB，DC，设AE所在直线为l，
∵l垂直于两底AB，DC，且l是平面ABCD内的直线，
∴l与梯形ABCD的两腰不垂直，因此必要性不成立．
故答案为：充分不必要．
∵四边形ABCD为梯形，AB∥CD，
∴两腰BC、AD所在直线是相交直线．
∵l垂直于两腰AD，BC
∴l⊥平面ABCD
又∵AB，DC是平面ABCD内的直线，
∴l垂直于两底AB，DC，因此充分性成立；
再看必要性
作出梯形ABCD的高AE，则AE垂直于两底AB，DC，设AE所在直线为l，
∵l垂直于两底AB，DC，且l是平面ABCD内的直线，
∴l与梯形ABCD的两腰不垂直，因此必要性不成立．
故答案为：充分不必要．
点评：本题借助于必要条件、充分条件与充要条件的判断，着重考查了空间直线与平面垂直、直线与直线垂直的判定与证明等知识点，属于基础题．
练习册系列答案
相关题目
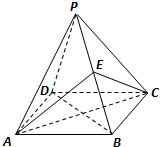（2012•盐城一模）如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PA=PC，E为PB的中点．