题目内容
(2012•盐城一模)在极坐标系中,圆C的方程为ρ=4
cos(θ-
),以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
(t为参数),求直线l被⊙C截得的弦AB的长度.
| 2 |
| π |
| 4 |
|
分析:先两边同乘以ρ,利用公式即可得到圆的圆心和半径,再将参数方程化为普通方程,结合直角坐标系下的点到直线的距离公式求解即得.
解答:解:⊙C的方程化为ρ=4cosθ+4sinθ,两边同乘以ρ,得ρ2=4ρcosθ+4ρsinθ
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得x2+y2-4x-4y=0…(5分)
其圆心C坐标为(2,2),半径r=2
,
又直线l的普通方程为x-y-2=0,
∴圆心C到直线l的距离d=
=
,
∴弦长AB=2
=2
…(10分)
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得x2+y2-4x-4y=0…(5分)
其圆心C坐标为(2,2),半径r=2
| 2 |
又直线l的普通方程为x-y-2=0,
∴圆心C到直线l的距离d=
| 2 | ||
|
| 2 |
∴弦长AB=2
| 8-2 |
| 6 |
点评:考查圆的极坐标方程、参数方程与普通方程的互化,点到直线的距离公式.要求学生能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.属于中等题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
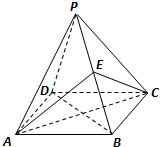 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.