题目内容
(2012•盐城一模)若关于x的方程kx+1=lnx有解,则实数k的取值范围是
(-∞,
]
| 1 |
| e2 |
(-∞,
]
.| 1 |
| e2 |
分析:设f(x)=lnx-kx-1,将方程kx+1=lnx有解问题转化为函数f(x)有零点问题,进而利用导数研究函数f(x)的单调性和极值,找到使函数有零点的k的范围
解答:解:设f(x)=lnx-kx-1
则f′(x)=
-k=
(x>0)
若k≤0,则f′(x)>0,f(x)为(0,+∞)上的增函数,∵x→0时,f(x)→-∞,∴f(x)有且只有一个零点,即此时方程kx+1=lnx有解
若k>0,则f(x)在(0,
)上为增函数,在(
,+∞)上为减函数
要使函数f(x)有零点,需f(
)≥0
即-lnk-2≥0
解得:k≤
∴0<k≤
时,f(x)有零点,即此时方程kx+1=lnx有解
综上所述:k≤
故答案为 (-∞,
]
则f′(x)=
| 1 |
| x |
| 1-kx |
| x |
若k≤0,则f′(x)>0,f(x)为(0,+∞)上的增函数,∵x→0时,f(x)→-∞,∴f(x)有且只有一个零点,即此时方程kx+1=lnx有解
若k>0,则f(x)在(0,
| 1 |
| k |
| 1 |
| k |
要使函数f(x)有零点,需f(
| 1 |
| k |
即-lnk-2≥0
解得:k≤
| 1 |
| e2 |
∴0<k≤
| 1 |
| e2 |
综上所述:k≤
| 1 |
| e2 |
故答案为 (-∞,
| 1 |
| e2 |
点评:本题主要考查了方程的根与函数零点间的关系,构造函数解决零点存在性问题的方法,导数在函数单调性和极值中的应用,转化化归的思想方法

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
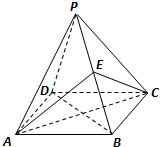 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.