题目内容
若存在实常数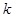 和
和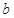 ,使得函数
,使得函数 和
和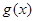 对其定义域上的任意实数
对其定义域上的任意实数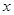 分别满足:
分别满足: 和
和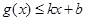 ,则称直线
,则称直线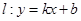 为
为 和
和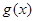 的“隔离直线”.已知函数
的“隔离直线”.已知函数 和函数
和函数 ,那么函数
,那么函数 和函数
和函数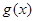 的隔离直线方程为_________.
的隔离直线方程为_________.

解析

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
题目内容
若存在实常数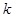 和
和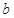 ,使得函数
,使得函数 和
和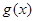 对其定义域上的任意实数
对其定义域上的任意实数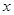 分别满足:
分别满足: 和
和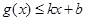 ,则称直线
,则称直线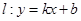 为
为 和
和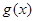 的“隔离直线”.已知函数
的“隔离直线”.已知函数 和函数
和函数 ,那么函数
,那么函数 和函数
和函数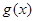 的隔离直线方程为_________.
的隔离直线方程为_________.

解析

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案