题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,令
时,令![]() ,其导函数为
,其导函数为![]() ,设
,设![]() 是函数
是函数![]() 的两个零点,判断
的两个零点,判断![]() 是否为
是否为![]() 的零点?并说明理由.
的零点?并说明理由.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(Ⅰ)先求导,再分类讨论,根据导数和函数单调性的关系即可求出,
(Ⅱ)由(Ⅰ)知,g(x)=x2﹣2lnx﹣x,x1,x2是函数g(x)的两个零点,不妨设0<x1<x2,可得x12﹣2lnx1﹣x1=0,x22﹣2lnx2﹣x2=0,两式相减化简可得x1+x2﹣1=![]() ,再对g(x)求导,判断
,再对g(x)求导,判断![]() 的符号即可证明
的符号即可证明
试题解析:
(1)依题意知函数![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
①当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,由
时,由![]() 得:
得: ![]() ,
,
则当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
(2)![]() 不是导函数
不是导函数![]() 的零点.
的零点.
证明如下:由(Ⅰ)知函数![]() .
.
∵![]() ,
, ![]() 是函数
是函数![]() 的两个零点,不妨设
的两个零点,不妨设![]() ,
,
∴![]() ,两式相减得:
,两式相减得: ![]()
即: ![]()
又![]() .
.
则![]()
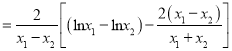 .
.
设![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
令![]() ,
, 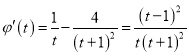 .
.
又![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上是増函数,
上是増函数,
则![]() ,即当
,即当![]() 时,
时, ![]() ,
,
从而![]() ,
,
又![]() 所以
所以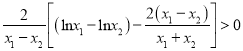 ,
,
故![]() ,所以
,所以![]() 不是导函数
不是导函数![]() 的零点.
的零点.

练习册系列答案
相关题目
【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中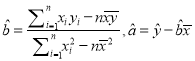
(注: ![]() )
)