题目内容
已知三次函数y = f (x)过点(–1,0),且f ′(x) = (x + 1)2,将y = f (x)的图象向右平移一个单位,再将各点的纵坐标变为原来的3倍得函数y = g (x)的图象,函数y = h (x)与y = g (x)的图象关于点M(2,0)对称.
(1)求y = h (x)的解析式;
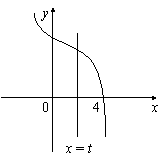 (2)若直线x = t
(0<t<4)将函数y = h (x)的图象与两坐标轴围成的图形的面积二等分,求t的值.
(2)若直线x = t
(0<t<4)将函数y = h (x)的图象与两坐标轴围成的图形的面积二等分,求t的值.
【答案】
【解析】(1)∵f ′(x)
=(x + 1)2 ∴设f (x) =
∵f (–1) =
0 ∴m = 0 ∴f (x) =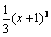 ∴g (x) = x3
……5分
∴g (x) = x3
……5分
设p(x,y)为函数h (x)图象上任一点,p关于M(2,0)对称点为p′(4 – x,y)
 ∵点p′在y = g (x)图象上 ∴y = (4 – x)3 即h (x) = (4 – x)3 ……8分
∵点p′在y = g (x)图象上 ∴y = (4 – x)3 即h (x) = (4 – x)3 ……8分
(2)如图,依题意知
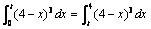 ……10分
……10分
∴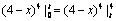
即(4 – t)4 – 44 = –(4 – t)4 (0< t < 4)
∴t = 4 – .
……12分
.
……12分

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
