题目内容
已知三次函数f(x)=ax3+bx2+cx+d,(a,b,c,d∈R),命题p:y=f(x)是R上的单调函数;命题q:y=f(x)的图象与x轴恰有一个交点.则p是q的( )
分析:结合三次函数的图象,利用充分条件和必要条件的定义判断.
解答:解:因为三次函数的值域为R,所以若y=f(x)是R上的单调函数,则y=f(x)的图象与x轴恰有一个交点成立.
则当a>0时,三次函数的极大值小于0或极小值大于0,y=f(x)的图象与x轴恰有一个交点,但此时函数不单调.
所以p是q充分不必要条件.
故选A.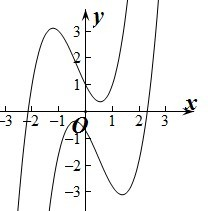
则当a>0时,三次函数的极大值小于0或极小值大于0,y=f(x)的图象与x轴恰有一个交点,但此时函数不单调.
所以p是q充分不必要条件.
故选A.

点评:本题主要考查充分条件和必要条件的判断,要求熟练掌握三次函数的图象.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则
已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则