题目内容
10.(1)解方程9x-3x+1-10=0;(2)已知x∈[$\frac{1}{2}$,8],求函数f(x)=(log2$\frac{x}{4}$)•(log2$\frac{2}{x}$)的值域.
分析 (1)令t=3x,(t>0),得到得t2-3t-10=0,解得即可;
(2)令t=log2x,因为x∈[$\frac{1}{2}$,8],所以t∈[-1,3],函数f(x)=g(t))=-(t-2)(t-1),根据二次函数的性质得到最值.
解答 解(1)令t=3x,(t>0),由9x-3x+1-10=0;
得t2-3t-10=0,解得t=5,或t=-2(舍去),
所以3x=5,解得x=log35,
(2)令t=log2x,因为x∈[$\frac{1}{2}$,8],所以t∈[-1,3],
又f(x)=(log2$\frac{x}{4}$)•(log2$\frac{2}{x}$)=(log2x-2)(1-log2x),
∴g(t)=-(t-2)(t-1)=-(t-$\frac{3}{2}$)2+$\frac{1}{4}$
当t=$\frac{3}{2}$时,g(t)max=$\frac{1}{4}$,
当t=-1时,g(t)min=-6,
所以函数f(x)的值域为[-6,$\frac{1}{4}$].
点评 本题考查了换元法求方程的解,以及求函数的值域,关键是换元,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
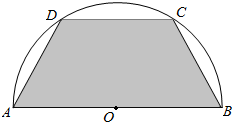 如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.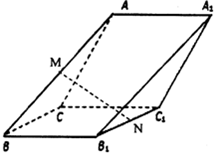 如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,
如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,