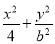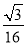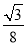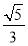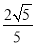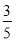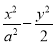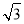Question

已知椭圆C的中心为平面直角坐标系xOy的原点，焦点在x轴上，它的一个顶点到两个焦点的距离分别是7和1.

(1)求椭圆C的方程；

(2)若P为椭圆C上的动点，M为过P且垂直于x轴的直线上的一点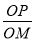，＝λ，求点M的轨迹方程，并说明轨迹是什么曲线．

 

Answer 1

（1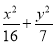）＝1（2）①当λ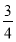＝时，轨迹方程为y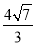＝± (－4≤x≤4)．轨迹是两条平行于x轴的线段．②当λ≠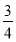时，方程变形为＝1，当0<λ<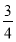时，点M的轨迹为中心在原点、实轴在y轴上的双曲线满足－4≤x≤4的部分；当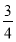<λ<1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆满足－4≤x≤4的部分；当λ≥1时，点M的轨迹为中心在原点，长轴在x轴上的椭圆．

【解析】(1)设椭圆长半轴长及半焦距分别为a，c，由已知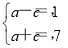得解得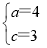又∵b2＝a2－c2，∴b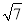＝，所以椭圆C的方程为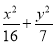＝1. ?

(2)设M(x，y)，其中x∈[－4,4]，由已知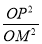＝λ2及点P在椭圆C上可得

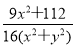＝λ2，整理得(16λ2－9)x2＋16λ2y2＝112，其中x∈[－4,4]．

①当λ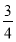＝时，化简得9y2＝112，所以点M的轨迹方程为y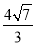＝± (－4≤x≤4)．轨迹是两条平行于x轴的线段．

②当λ≠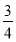时，方程变形为＝1，其中x∈[－4,4]．当0<λ<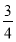时，点M的轨迹为中心在原点、实轴在y轴上的双曲线满足－4≤x≤4的部分；当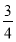<λ<1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆满足－4≤x≤4的部分；当λ≥1时，点M的轨迹为中心在原点，长轴在x轴上的椭圆．