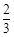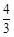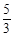题目内容
已知函数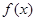
在R上满足f(x)=2f(4-x)-2x2+5x，则曲线
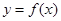在点(2,f(2) )
处的切线方程是（ ）
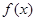在R上满足f(x)=2f(4-x)-2x2+5x，则曲线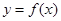在点(2,f(2) )处的切线方程是（ ）
| A．y=-x | B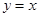． | C．y="-x" +4 | D．y="-2x+2" |
A
因为解：∵f（x）=2f（4-x）-2x2+5x，
∴f（4-x）=2f（x）-（4-x）2+5（4-x）
∴f（2-x）=2f（x）-x2+8x+4-5x
将f（4-x）代入f（x）=2f（4-x）-2x2+5x
得f（x），y=f（x）在（2，f（2））处的切线斜率为y′=-1．
∴函数y=f（x）在（2，f（2））处的切线方程为．y=-x
答案A
∴f（4-x）=2f（x）-（4-x）2+5（4-x）
∴f（2-x）=2f（x）-x2+8x+4-5x
将f（4-x）代入f（x）=2f（4-x）-2x2+5x
得f（x），y=f（x）在（2，f（2））处的切线斜率为y′=-1．
∴函数y=f（x）在（2，f（2））处的切线方程为．y=-x
答案A
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数
在
上的单调性;
,使曲线
在点
处的切线与
轴垂直?若存在,求出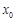
的值;若不存在,请说明理由. 
与时间t（
）的关系近似表示为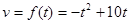
，则汽车在时刻
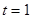秒时的加速度为 （ ）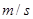
，
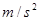
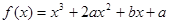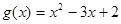，其中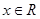
，a、b为常数，已知曲线
在点（2,0）处有相同的切线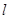
。
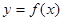单调区间与极值。
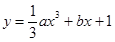，其中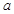
为2，4，6，8中的任意一个，
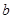为1，3，5，7中的任意一个。现从这些曲线中任取两条，它们在
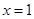处的切线相互平行的组数为
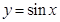和
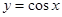的交点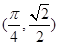
处，两切线的斜率之积等于 .
是函数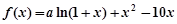
的一个极值点。
的值；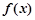
的单调区间；
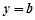与函数
的图象有3个交点，求
的取值范围。
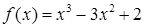在区间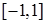
上的最大值是_________. 
，
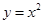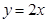围成的封闭图形的面积为( )
