题目内容
已知函数f(x)= m(x-1)2-2x+3+lnx,m∈R.
m(x-1)2-2x+3+lnx,m∈R.
(1)当m=0时,求函数f(x)的单调增区间;
(2)当m>0时,若曲线y=f(x)在点P(1,1)处的切线l与曲线y=f(x)有且只有一个公共点,求实数m的值.
解:(1)当m=0时,函数f(x)=-2x+3+lnx
由题意知x>0,f′(x)=-2+ =
=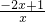 ,令f′(x)>0,得0<x<
,令f′(x)>0,得0<x< 时,
时,
所以f(x)的增区间为(0, ).
).
(2)由f′(x)=mx-m-2+ ,得f′(1)=-1,
,得f′(1)=-1,
知曲线y=f(x)在点P(1,1)处的切线l的方程为y=-x+2,
于是方程:-x+2=f(x)即方程 m(x-1)2-x+1+lnx=0有且只有一个实数根;
m(x-1)2-x+1+lnx=0有且只有一个实数根;
设g(x)= m(x-1)2-x+1+lnx,(x>0).
m(x-1)2-x+1+lnx,(x>0).
则g′(x)=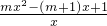 =
=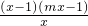 ,
,
①当m=1时,g′(x)=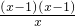 ≥0,g(x)在(0,+∞)上为增函数,且g(1)=0,故m=1符合题设;
≥0,g(x)在(0,+∞)上为增函数,且g(1)=0,故m=1符合题设;
②当m>1时,由g′(x)>0得0<x< 或x>1,
或x>1,
由g′(x)=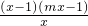 <0得
<0得 <x<1,
<x<1,
故g(x)在区间(0, ),(1,+∞)上单调递增,在( 1,
),(1,+∞)上单调递增,在( 1, )区间单调递减,
)区间单调递减,
又g(1)=0,且当x→0时,g(x)→-∞,此时曲线y=g(x)与x轴有两个交点,故m>1不合题意;
③当0<m<1时,由g′(x)=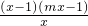 >0得0<x<1或x>
>0得0<x<1或x> ,
,
由g′(x)=<0得1<x< ,
,
故g(x)在区间(0,1),(1, )上单调递增,在(
)上单调递增,在( ,+∞)区间单调递减,
,+∞)区间单调递减,
又g(1)=0,且当x→0时,g(x)→+∞,此时曲线y=g(x)与x轴有两个交点,故0<m<1不合题意;
∴由上述知:m=1.
分析:(1)求出f′(x),在定义域内解不等式f′(x)>0,即得f(x)的单调增区间;
(2)先求切线方程为y=-x+2,再由切线L与C有且只有一个公共点,转化为 m(x-1)2-x+1+lnx=0有且只有一个实数解,从而可求实数m的范围.
m(x-1)2-x+1+lnx=0有且只有一个实数解,从而可求实数m的范围.
点评:本题考查应用导数研究函数的单调性、最值问题,考查分析问题解决问题的能力,考查转化思想.
由题意知x>0,f′(x)=-2+
 =
=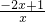 ,令f′(x)>0,得0<x<
,令f′(x)>0,得0<x< 时,
时,所以f(x)的增区间为(0,
 ).
).(2)由f′(x)=mx-m-2+
 ,得f′(1)=-1,
,得f′(1)=-1,知曲线y=f(x)在点P(1,1)处的切线l的方程为y=-x+2,
于是方程:-x+2=f(x)即方程
 m(x-1)2-x+1+lnx=0有且只有一个实数根;
m(x-1)2-x+1+lnx=0有且只有一个实数根;设g(x)=
 m(x-1)2-x+1+lnx,(x>0).
m(x-1)2-x+1+lnx,(x>0).则g′(x)=
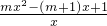 =
=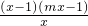 ,
,①当m=1时,g′(x)=
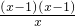 ≥0,g(x)在(0,+∞)上为增函数,且g(1)=0,故m=1符合题设;
≥0,g(x)在(0,+∞)上为增函数,且g(1)=0,故m=1符合题设;②当m>1时,由g′(x)>0得0<x<
 或x>1,
或x>1,由g′(x)=
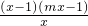 <0得
<0得 <x<1,
<x<1,故g(x)在区间(0,
 ),(1,+∞)上单调递增,在( 1,
),(1,+∞)上单调递增,在( 1, )区间单调递减,
)区间单调递减,又g(1)=0,且当x→0时,g(x)→-∞,此时曲线y=g(x)与x轴有两个交点,故m>1不合题意;
③当0<m<1时,由g′(x)=
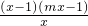 >0得0<x<1或x>
>0得0<x<1或x> ,
,由g′(x)=<0得1<x<
 ,
,故g(x)在区间(0,1),(1,
 )上单调递增,在(
)上单调递增,在( ,+∞)区间单调递减,
,+∞)区间单调递减,又g(1)=0,且当x→0时,g(x)→+∞,此时曲线y=g(x)与x轴有两个交点,故0<m<1不合题意;
∴由上述知:m=1.
分析:(1)求出f′(x),在定义域内解不等式f′(x)>0,即得f(x)的单调增区间;
(2)先求切线方程为y=-x+2,再由切线L与C有且只有一个公共点,转化为
 m(x-1)2-x+1+lnx=0有且只有一个实数解,从而可求实数m的范围.
m(x-1)2-x+1+lnx=0有且只有一个实数解,从而可求实数m的范围.点评:本题考查应用导数研究函数的单调性、最值问题,考查分析问题解决问题的能力,考查转化思想.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目