题目内容
已知函数f(x十1)是定义在R上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式 恒成立,则不等式f(1-x)<0的解集为( )
恒成立,则不等式f(1-x)<0的解集为( )
A.(1,+ ) ) | B.(一 ,0) ,0) | C.(0,+ ) ) | D.(一 ,1) ,1) |
B
解析试题分析:因为函数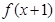 是定义在R上的奇函数,所以函数
是定义在R上的奇函数,所以函数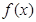 满足
满足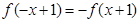 .又因为不等式
.又因为不等式 恒成立,所以可得
恒成立,所以可得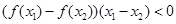 .所以函数
.所以函数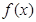 在R上递减,求
在R上递减,求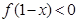 的解集等价于
的解集等价于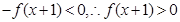 ,又由函数
,又由函数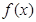 在R上递减,且函数
在R上递减,且函数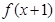 是定义在R上的奇函数.所以
是定义在R上的奇函数.所以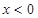 故选B.
故选B.
考点:1.函数的性质.2.隐函数的性质.3.函数的单调性.4.函数的图像的应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
对于任意不全为 的实数
的实数 ,关于
,关于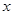 的方程
的方程 在区间
在区间 内( )
内( )
| A.无实根 | B.恰有一实根 | C.至少有一实根 | D.至多有一实根 |
已知 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.己知在过滤过程中废气中的污染物数量尸(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:P=P0e-kt,(k,P0均为正的常数).若在前5个小时的过滤过程中污染物被排除了90%.那么,至少还需( )时间过滤才可以排放.
A. 小时 小时 | B. 小时 小时 | C.5小时 | D.10小时 |
已知函数 的值域是
的值域是 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 ,若对于任意
,若对于任意 ,当
,当 时,总有
时,总有 ,则区间
,则区间 有可能是( )
有可能是( )
A. | B. | C.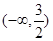 | D. |
如图,A,B,C,D是某煤矿的四个采煤点,m是公路,图中所标线段为道路,ABQP,BCRQ,CDSR近似于正方形.已知A,B,C,D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的质量都成正比.现要从P,Q,R,S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )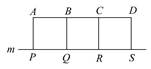
| A.P点 | B.Q点 | C.R点 | D.S点 |
函数f(x)= 的图象和g(x)=log2x的图象的交点个数是( )
的图象和g(x)=log2x的图象的交点个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知函数f(x)= 若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是( )
若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是( )
| A.(-∞,0) | B.(-∞,0)∪(0,1) |
| C.(0,1) | D.(0,1)∪(1,+∞) |