题目内容
已知 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
B
解析试题分析: ,
, 是幂函数
是幂函数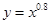 的两个函数值,因0.8>0,所以幂函数
的两个函数值,因0.8>0,所以幂函数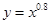 在[0,+∞)是增函数,因1.1>0.8>0,所以
在[0,+∞)是增函数,因1.1>0.8>0,所以 >
> >
>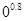 =0,即
=0,即 ,因对数函数
,因对数函数 是增函数,故
是增函数,故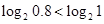 =0,故
=0,故 ,所以
,所以 .∵幂函数
.∵幂函数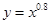 在(0,+∞)是增函数,0.7<1.1,∴
在(0,+∞)是增函数,0.7<1.1,∴ ,又∵
,又∵ ,∴
,∴ ,故选B.
,故选B.
考点:幂函数的单调性,对数函数的性质

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
若函数 ,若
,若 ,则实数
,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C.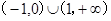 | D. |
已知函数f(x十1)是定义在R上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式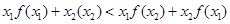 恒成立,则不等式f(1-x)<0的解集为( )
恒成立,则不等式f(1-x)<0的解集为( )
A.(一 ,0) ,0) | B.(0,+ ) ) | C.(一 ,1) ,1) | D.(1,+ ) ) |
已知函数f(x十1)是定义在R上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式 恒成立,则不等式f(1-x)<0的解集为( )
恒成立,则不等式f(1-x)<0的解集为( )
A.(1,+ ) ) | B.(一 ,0) ,0) | C.(0,+ ) ) | D.(一 ,1) ,1) |
某银行准备新设一种定期存款业务,经预算,存款量与存款利率的平
方成正比,比例系数为k(k>0),贷款的利率为0.048,假设银行吸收的存款能全部放贷出去.若存款利率为x(x∈(0,0.048)),则x为多少时,银行可获得最大收益 ( ).
| A.0.016 | B.0.032 |
| C.0.024 | D.0.048 |
设f(x)= g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
| A.(-∞,-1]∪[1,+∞) | B.(-∞,-1]∪[0,+∞) |
| C.[0,+∞) | D.[1,+∞) |
已知函数f(x)=ax2+bx+c,且a>b>c,a+b+c=0,则( )
| A.?x∈(0,1),都有f(x)>0 |
| B.?x∈(0,1),都有f(x)<0 |
| C.?x0∈(0,1),使得f(x0)=0 |
| D.?x0∈(0,1),使得f(x0)>0 |
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A.16 | B.-16 |
| C.a2-2a-16 | D.a2+2a-16 |
化简 (x<0,y<0)得( )
(x<0,y<0)得( )
| A.2x2y | B.2xy | C.4x2y | D.-2x2y |