题目内容
【题目】已知直线![]() 与函数
与函数![]() (
(![]() )的图象相交,将其中三个相邻交点从左到右依次记为A,B,C,且满足
)的图象相交,将其中三个相邻交点从左到右依次记为A,B,C,且满足![]()
![]() 有下列结论:
有下列结论:
①n的值可能为2
②当![]() ,且
,且![]() 时,
时,![]() 的图象可能关于直线
的图象可能关于直线![]() 对称
对称
③当![]() 时,有且仅有一个实数ω,使得
时,有且仅有一个实数ω,使得![]() 在
在![]() 上单调递增;
上单调递增;
④不等式![]() 恒成立
恒成立
其中所有正确结论的编号为( )
A.③B.①②C.②④D.③④
【答案】D
【解析】
根据三角函数的图像性质,依次分析四个结论即可求解.
解析:如图所示,
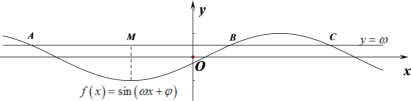
不妨设![]() ,
,![]() ,
,![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,
,
显然有![]() ,
,![]() ,且
,且![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
∵![]()
![]() ,∴
,∴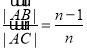
![]() ,
,
∴![]() ,即
,即![]() ,(1)
,(1)
∵![]() ,且
,且![]() ,∴由正弦曲线的图像可知,
,∴由正弦曲线的图像可知,
![]() (
(![]() ).
).
∴![]() (
(![]() ),
),
即![]() ,(2)
,(2)
由等式(1),(2)可得![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,且
,且![]() ,∴
,∴![]() ,且
,且![]() ,
,
对于结论①,显然![]() ,故结论①错误:
,故结论①错误:
对于结论②,当![]() ,且
,且![]() 时,则
时,则![]() ,
,
故![]() ,若
,若![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
则![]() (
(![]() ),即
),即![]() (
(![]() )
)
显然与![]() 矛盾,从而可知结论②错误:
矛盾,从而可知结论②错误:
对于结论③,∵![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴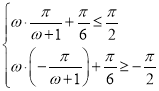 ,∴
,∴![]() ,故结论③正确;
,故结论③正确;
对于结论④,下证不等式![]() (
(![]() ),
),
(法一)当![]() 时,
时,![]() ,
,
∴![]() (
(![]() ),即
),即![]() (
(![]() ),
),
(法二)即证不等式![]() (
(![]() )恒成立,
)恒成立,
构造函数![]() (
(![]() ),显然函数
),显然函数![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,即不等式
,即不等式![]() (
(![]() )恒成立,故结论④正确:
)恒成立,故结论④正确:
综上所述,正确的结论编号为③④
故选:D

练习册系列答案
相关题目