Question

2．已知点O（0，0），A（3，1），点P（x，y）满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-2y+4≥0}\\{3x-y-3≤0}\end{array}\right.$，求$\overrightarrow{OA}•\overrightarrow{OP}$的最大值和最小值．

Answer 1

分析 由约束条件作出可行域，利用数量积的坐标表示求得$\overrightarrow{OA}•\overrightarrow{OP}$，得到线性目标函数，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．

解答 解：由约束条件$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-2y+4≥0}\\{3x-y-3≤0}\end{array}\right.$作出可行域如图，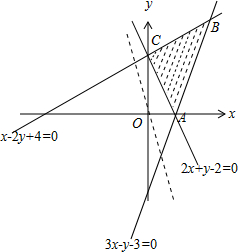

又$\overrightarrow{OA}•\overrightarrow{OP}=（3，1）•（x，y）=3x+y$，
设z=3x+y，
联立$\left\{\begin{array}{l}{x-2y+4=0}\\{3x-y-3=0}\end{array}\right.$，解得：B（2，3），
又C（2，3），
化目标函数z=3x+y为y=-3x+z，
由图可知，当直线y=-3x+z过C时，z_min=2；
当直线y=-3x+z过B时，z_max=9．

点评 本题考查简单的线性规划，考查了平面向量的数量积运算，体现了数形结合的解题思想方法，是中档题．