题目内容
设数列{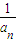 }是等差数列,且a2a4+a4a6+a6a2=1,a2a4a6=
}是等差数列,且a2a4+a4a6+a6a2=1,a2a4a6= ,则a10=( )
,则a10=( )A.1
B.-1
C.
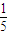
D.-1或
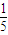
【答案】分析:设等差数列{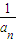 }的公差为d,
}的公差为d,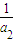 =
=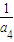 -2d,
-2d,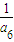 =
=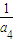 +2d,由a2a4+a4a6+a6a2=1,a2a4a6=
+2d,由a2a4+a4a6+a6a2=1,a2a4a6= ,可求得
,可求得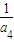 =
= ,d=
,d= ,从而可求得a10.
,从而可求得a10.
解答:解:设等差数列{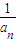 }的公差为d,
}的公差为d,
∵a2a4+a4a6+a6a2=1,a2a4a6= ,
,
∴等式两端同除以a2a4a6得: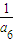 +
+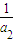 +
+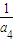 =
=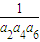 =6,
=6,
∴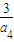 =6,
=6,
∴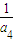 =2;
=2;
∴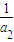 •
•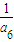 =
= ,即(
,即(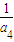 -2d)(
-2d)(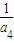 +2d)=
+2d)= ,
,
∴d= 或d=-
或d=- (舍).
(舍).
∴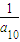 =
=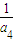 +6d=2+6×
+6d=2+6× =5,
=5,
∴a10=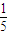 .
.
故选C.
点评:本题考查等差数列与等比数列的综合,求得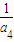 =
= ,d=
,d= 是关键,考查推理与分析及运算能力,属于中档题.
是关键,考查推理与分析及运算能力,属于中档题.
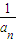 }的公差为d,
}的公差为d,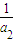 =
=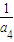 -2d,
-2d,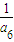 =
=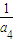 +2d,由a2a4+a4a6+a6a2=1,a2a4a6=
+2d,由a2a4+a4a6+a6a2=1,a2a4a6= ,可求得
,可求得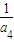 =
= ,d=
,d= ,从而可求得a10.
,从而可求得a10.解答:解:设等差数列{
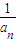 }的公差为d,
}的公差为d,∵a2a4+a4a6+a6a2=1,a2a4a6=
 ,
,∴等式两端同除以a2a4a6得:
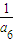 +
+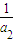 +
+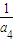 =
=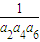 =6,
=6,∴
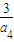 =6,
=6,∴
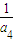 =2;
=2;∴
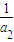 •
•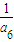 =
= ,即(
,即(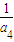 -2d)(
-2d)(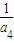 +2d)=
+2d)= ,
,∴d=
 或d=-
或d=- (舍).
(舍).∴
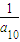 =
=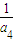 +6d=2+6×
+6d=2+6× =5,
=5,∴a10=
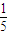 .
.故选C.
点评:本题考查等差数列与等比数列的综合,求得
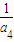 =
= ,d=
,d= 是关键,考查推理与分析及运算能力,属于中档题.
是关键,考查推理与分析及运算能力,属于中档题. 
练习册系列答案
相关题目
设数列{an}是等差数列,且a2=-8,a15=5,Sn是数列{an}的前n项和,则( )
| A、S10=S11 | B、S10>S11 | C、S9=S10 | D、S9<S10 |