题目内容
设数列{an}是等差数列,a1+a2+a3=-24,a19=26,则此数列{an}前20项和等于
180
180
.分析:由等差数列的性质可得:a2+a19=18,而S20=
=10(a1+a20)=10(a2+a19),代入即可.
| 20(a1+a20) |
| 2 |
解答:解:由等差数列的性质可得:a1+a2+a3=3a2=-24,即a2=-8,
故a2+a19=-8+26=18,由等差数列的求和公式可得:
数列{an}前20项和S20=
=10(a1+a20)=10(a2+a19)=10×18=180.
故答案为:180
故a2+a19=-8+26=18,由等差数列的求和公式可得:
数列{an}前20项和S20=
| 20(a1+a20) |
| 2 |
故答案为:180
点评:本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
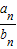 }的前n项和Sn.
}的前n项和Sn.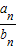 }的前n项和Sn.
}的前n项和Sn.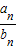 }的前n项和Sn.
}的前n项和Sn.