题目内容
设数列{an}是等差数列，且a3=-6，a7=6，Sn是数列{an}的前n项和，则（ ）
分析：已知a3=-6，a7=6，利用等差数列的通项公式求出公差及首项，利用通项公式求出通项，判断出第5项为0，即可得到结论．
解答：解：设数列{an}的公差为d
∵a3=-6，a7=6，∴d=
=3
∵a3=a1+2d，∴a1=-12
∴an=a1+（n-1）d=3n-15
∴a5=0，∴S4=S5
故选A．
∵a3=-6，a7=6，∴d=
| a7-a3 |
| 7-3 |
∵a3=a1+2d，∴a1=-12
∴an=a1+（n-1）d=3n-15
∴a5=0，∴S4=S5
故选A．
点评：本题考查数列的通项，考查学生分析解决问题的能力，解决有关等差数列、等比数列的问题，一般的思路是围绕通项及前n项和公式列出方程组，解方程组，求出基本量．
练习册系列答案
名校课堂系列答案
相关题目
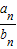}的前n项和Sn．
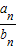}的前n项和Sn．
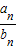}的前n项和Sn．