题目内容
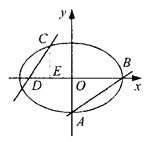
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)直线方程![]() 为:
为:![]()
![]()
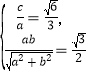
![]()
![]()
![]() 椭圆方程为
椭圆方程为![]() ;(2)假若存在这样的
;(2)假若存在这样的![]() 值,由
值,由![]()
![]()
![]()
![]() .
.
![]()
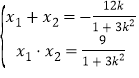
![]()
![]() .要使以
.要使以![]() 为直径的圆过点
为直径的圆过点![]()
![]() 当且仅当
当且仅当![]() 时
时![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 存在
存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.
试题解析:(1)直线方程![]() 为:
为:![]() .
.
依题意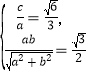 解得
解得![]()
∴ 椭圆方程为![]()
(2)假若存在这样的![]() 值,由
值,由![]() 得
得![]()
![]() .
.
![]()
![]() . ①
. ①
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则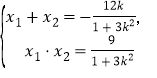 ②
②
而![]() .
.
要使以![]() 为直径的圆过点
为直径的圆过点![]() ,当且仅当
,当且仅当![]() 时,则
时,则![]() ,即
,即![]() .
.
![]()
![]() . ③
. ③
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
,使①成立.
综上可知,存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
