题目内容
已知函数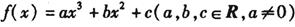 的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.
的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.
(2) 若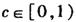 ,试求函数f(x)的单调区间;
,试求函数f(x)的单调区间;
(3) 若a>0,b>0且(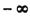 ,m),(n,
,m),(n,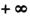 )是f(x)的单调递增区间,试求n-m-2c的范围
)是f(x)的单调递增区间,试求n-m-2c的范围
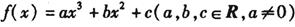 的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.
的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.(2) 若
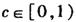 ,试求函数f(x)的单调区间;
,试求函数f(x)的单调区间;(3) 若a>0,b>0且(
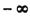 ,m),(n,
,m),(n,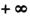 )是f(x)的单调递增区间,试求n-m-2c的范围
)是f(x)的单调递增区间,试求n-m-2c的范围


略

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 设函数
设函数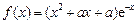 有极值.
有极值. ,试确定
,试确定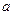 ;
;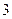 时,只限于
时,只限于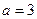 的情况.
的情况.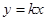 与曲线
与曲线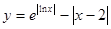 有3个公共点时,实数
有3个公共点时,实数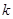 的取值范围是
的取值范围是 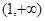
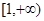

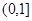
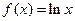 ,
,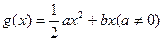
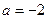 时,函数
时,函数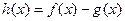 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;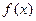 的图象
的图象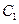 与函数
与函数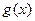 的图象
的图象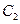 交于点
交于点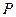 、
、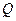 ,过线段
,过线段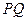 的中点
的中点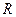 作
作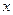 轴的垂线分别交
轴的垂线分别交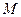 、
、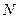 ,问是否存在点
,问是否存在点 小题满分10分)
小题满分10分) 盖长方体水池
盖长方体水池 ,底面一边长固定为8
,底面一边长固定为8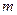 ,
, 最大装水量为72
最大装水量为72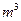 ,池底和池壁的造价分别为
,池底和池壁的造价分别为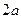 元
元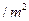 、
、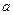 元
元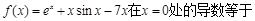
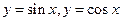 与直线
与直线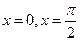 围成区域的面积为 .
围成区域的面积为 .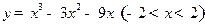 有( )
有( )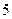 ,极小值
,极小值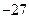 B 极大值
B 极大值