题目内容
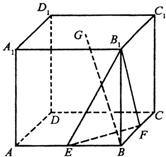 在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱AB和BC的中点,G为上底面A1B1C1D1的中心.
在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱AB和BC的中点,G为上底面A1B1C1D1的中心.(I)求AD与BG所成角的余弦值;
(II)求二面角B-FB1-E的大小;
(III)求点D到平面B1EF的距离.
分析:(I)以D为坐标原点,建立如图所示的空间直角坐标系,分别求出AD与BG的方向向量,代入向量夹角公式,即可求出AD与BG所成角的余弦值;
(II)分别求出平面B1EF的法向量和平面BFB1的法向量,代入向量夹角公式,即可求出二面角B-FB1-E的大小;
(III)由(II)中结论,平面B1EF的法向量
=(2,2,-1),又由
=(a,a,a).代入d=
,即可求出点D到平面B1EF的距离.
(II)分别求出平面B1EF的法向量和平面BFB1的法向量,代入向量夹角公式,即可求出二面角B-FB1-E的大小;
(III)由(II)中结论,平面B1EF的法向量
| m |
| DB1 |
|
| ||||
|
|
解答: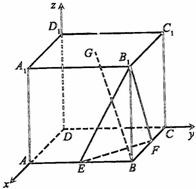 解:建立如图所示的空间直角坐标系D-xyz.
解:建立如图所示的空间直角坐标系D-xyz.
则A(a,0,0),B(a,a,0),C(0,a,0),E(a,
,0),F(
,a,0),B1(a,a,a),G(
,
,a),
(I)∵
=(-a,0,0),
=(-
,-
,a),
令AD与BG所成角为θ,
∴cosθ=
=
.
∴AD与BG所成角的余弦值为
.
(II)设平面B1EF的法向量为
=(x,y,z).
∵
=(-
,
,0),
=(0,
,0)
则
•
=0,
•
=0.
∴
取y=2,则x=2,z=-1.
∴可取
=(2,2,-1),
显然DC⊥平面BFB1.∴可取平面BFB1的法向量
=(0,1,0)
∴cos<
,
>=
=
.
∴所求二面角的大小为arccos
.
(III)由(II)已求平面B1EF的法向量
=(2,2,-1),又
=(a,a,a).
∴点D到平面B1EF的距离d=
=a.
∴点D到平面B1EF的距离为a.
 解:建立如图所示的空间直角坐标系D-xyz.
解:建立如图所示的空间直角坐标系D-xyz.则A(a,0,0),B(a,a,0),C(0,a,0),E(a,
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
(I)∵
| AD |
| BG |
| a |
| 2 |
| a |
| 2 |
令AD与BG所成角为θ,
∴cosθ=
| ||||
|
|
| ||
| 6 |
∴AD与BG所成角的余弦值为
| ||
| 6 |
(II)设平面B1EF的法向量为
| m |
∵
| EF |
| a |
| 2 |
| a |
| 2 |
| EB1 |
| a |
| 2 |
则
| m |
| EF |
| m |
| EB1 |
∴
|
取y=2,则x=2,z=-1.
∴可取
| m |
显然DC⊥平面BFB1.∴可取平面BFB1的法向量
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 2 |
| 3 |
∴所求二面角的大小为arccos
| 2 |
| 3 |
(III)由(II)已求平面B1EF的法向量
| m |
| DB1 |
∴点D到平面B1EF的距离d=
|
| ||||
|
|
∴点D到平面B1EF的距离为a.
点评:本题考查的知识点是用空间向量求平面间的夹角,异面直线及其所成的角,点到平面之间的距离,其中(I)的关键是求出AD与BG的方向向量,(II)的关键是求出平面B1EF的法向量和平面BFB1的法向量,(III)的关键是求出平面B1EF的法向量
=(2,2,-1),及D与平面B1EF任一点连线的方向向量,如
=(a,a,a).
| m |
| DB1 |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目

