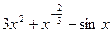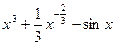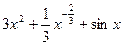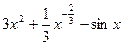题目内容
已知函数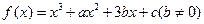 ,且
,且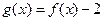 是奇函数.
是奇函数.
(Ⅰ)求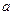 ,
,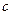 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数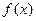 的单调区间.
的单调区间.
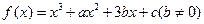 ,且
,且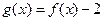 是奇函数.
是奇函数.(Ⅰ)求
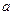 ,
,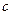 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数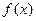 的单调区间.
的单调区间.解:(Ⅰ)因为函数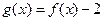 为奇函数,
为奇函数,
所以,对任意的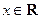 ,
,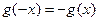 ,即
,即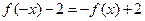 .…………………2分
.…………………2分
又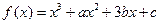 所以
所以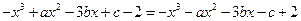 .
.
所以 解得
解得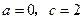 .………………………6分
.………………………6分
(Ⅱ)由(Ⅰ)得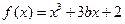 .所以
.所以 .………………8分
.………………8分
当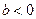 时,由
时,由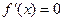 得
得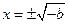 .
.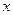 变化时,
变化时,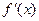 的变化情况如下表:
的变化情况如下表:
……………·············…………10分
所以,当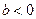 时,函数
时,函数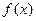 在
在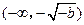 上单调递增,在
上单调递增,在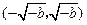 上单调递减,
上单调递减,
在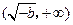 上单调递增.………………………12分
上单调递增.………………………12分
当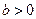 时,
时,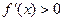 ,所以函数
,所以函数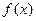 在
在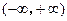 上单调递增.………………………14分
上单调递增.………………………14分
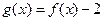 为奇函数,
为奇函数,所以,对任意的
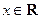 ,
,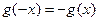 ,即
,即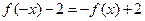 .…………………2分
.…………………2分又
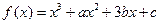 所以
所以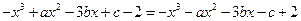 .
.所以
 解得
解得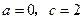 .………………………6分
.………………………6分(Ⅱ)由(Ⅰ)得
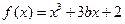 .所以
.所以 .………………8分
.………………8分当
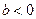 时,由
时,由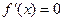 得
得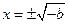 .
.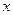 变化时,
变化时,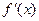 的变化情况如下表:
的变化情况如下表: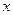 | 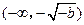 | 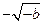 | 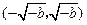 | 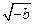 | 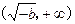 |
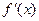 | 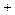 | 0 | 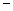 | 0 | 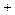 |
所以,当
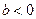 时,函数
时,函数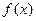 在
在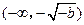 上单调递增,在
上单调递增,在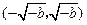 上单调递减,
上单调递减,在
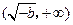 上单调递增.………………………12分
上单调递增.………………………12分当
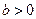 时,
时,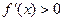 ,所以函数
,所以函数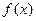 在
在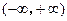 上单调递增.………………………14分
上单调递增.………………………14分略

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
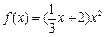 .
.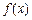 的导数
的导数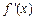 ;
;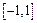 上的最大值与最小值.
上的最大值与最小值. 
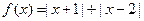 .
.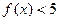 成立,求实数
成立,求实数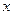 的取值范围;
的取值范围;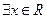 满足不等式
满足不等式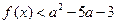 ,求实数
,求实数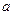 取值范围.
取值范围.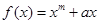 的导数为
的导数为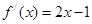 ,则数列
,则数列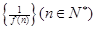 的前
的前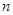 项和是 .
项和是 .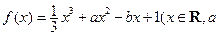 ,
,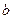 为实数)有极值,且在
为实数)有极值,且在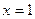 处的切线与直线
处的切线与直线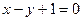 平行.
平行. (II)是否存在实数a,使得函数
(II)是否存在实数a,使得函数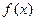 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存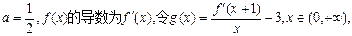
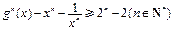 .
.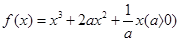 ,则
,则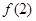 的最小值为
的最小值为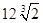
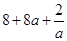
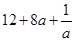
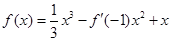 ,则(
,则(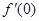 +
+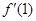 )
) =
=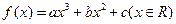 的图象与直线
的图象与直线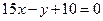 相切于点
相切于点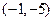 ,且函数
,且函数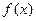 在
在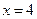 处取得极值。(1)求
处取得极值。(1)求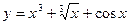 ,则
,则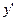 等于 ( )
等于 ( )